Bài tập 40 tr 129 sách GK Toán lớp 9 Tập 2
Hãy tính diện tích toàn phần của các hình tương ứng theo các kích thước đã cho trên hình 115.
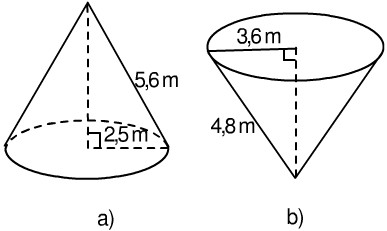
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Diện tích xung quanh của hình nón: \(S_{xq}=\pi rl.\)
+) Diện tích toàn phần của hình nón: \(S_{tp}=\pi rl + \pi r^2.\)
Lời giải chi tiết
- Với hình a:
\({S_{tp}} = {\rm{ }}{S_{xq}} + {\rm{ }}{S_{đáy}} = {\rm{ }}\pi rl{\rm{ }} + {\rm{ }}\pi {r^2}\)
\(= {\rm{ }}\pi {\rm{ }}.{\rm{ }}2,5{\rm{ }}.{\rm{ }}5,6{\rm{ }} + {\rm{ }}\pi {\rm{ }}.{\rm{ }}2,{5^2} \approx {\rm{ }}63,59{\rm{ }}({m^2})\)
- Với hình b:
\({S_{tp}} = {\rm{ }}{S_{xq}} + {\rm{ }}{S_{đáy}} = {\rm{ }}\pi {\rm{ }}.{\rm{ }}3,6{\rm{ }}.{\rm{ }}4,8{\rm{ }} + {\rm{ }}\pi {\rm{ }}.{\rm{ }}3,{6^2} \)
\( \approx {\rm{ }}94,95{\rm{ }}({m^2})\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 38 trang 129 SGK Toán 9 Tập 2
Bài tập 39 trang 129 SGK Toán 9 Tập 2
Bài tập 41 trang 129 SGK Toán 9 Tập 2
Bài tập 42 trang 130 SGK Toán 9 Tập 2
Bài tập 43 trang 130 SGK Toán 9 Tập 2
Bài tập 44 trang 130 SGK Toán 9 Tập 2
Bài tập 42 trang 174 SBT Toán 9 Tập 2
Bài tập 43 trang 174 SBT Toán 9 Tập 2
Bài tập 44 trang 174 SBT Toán 9 Tập 2
Bài tập 45 trang 174 SBT Toán 9 Tập 2
Bài tập 46 trang 175 SBT Toán 9 Tập 2
Bài tập 47 trang 175 SBT Toán 9 Tập 2
Bài tập 48 trang 175 SBT Toán 9 Tập 2
Bài tập 49 trang 175 SBT Toán 9 Tập 2
Bài tập IV.1 trang 176 SBT Toán 9 Tập 2
Bài tập IV.2 trang 176 SBT Toán 9 Tập 2
Bài tập IV.3 trang 176 SBT Toán 9 Tập 2
Bài tập IV.4 trang 177 SBT Toán 9 Tập 2
-


Có đường tròn tâm \(O,\) bán kính \(R = 5\;cm\) có dây cung \(AB = 6\;cm.\) Tính khoảng cách \(d\) từ \(O\) tới đường thẳng \(AB.\)
bởi Hoa Hong
 12/07/2021
12/07/2021
A. \(d = 1\;cm.\)
B. \(d = 2\;cm.\)
C. \(4cm.\)
D. \(d = \sqrt {34} \;cm.\)
Theo dõi (0) 1 Trả lời -


A. \(\cos B = \dfrac{{AB}}{{BC}}\)
B. \(\cos B = \dfrac{{AC}}{{BC}}\)
C. \(\cos B = \dfrac{{AB}}{{AC}}\)
D. \(\cos B = \dfrac{{AC}}{{AB}}.\)
Theo dõi (0) 1 Trả lời -


Cho đường tròn \(\left( O \right)\) đường kính AB và điểm C trên đường tròn \(\left( {C \ne A;C \ne B} \right)\). Gọi D là một điểm trên cung nhỏ \(CB\,\,\left( {D \ne C;D \ne B} \right)\) ; E là giao điểm của AD và BC; I là hình chiếu vuông góc của E trên AB; M là điểm thứ hai của đường thẳng DI và đường tròn \(\left( O \right)\).
bởi Nguyễn Thanh Hà
 11/07/2021
11/07/2021
1) Chứng minh tứ giác BDEI là tứ giác nội tiếp và \(CM \bot AB\).
2) Gọi K là giao điểm của BC và DM. Chứng minh \(BK.CE = BC.EK\)
Theo dõi (0) 1 Trả lời -


Cho hình trụ có bán kính đáy là bằng 9cm, diện tích xung quanh bằng \(198\pi \,\,c{m^2}\) , chiều cao hình trụ đó bằng
bởi Van Dung
 12/07/2021
12/07/2021
A. 9 cm.
B. 11 cm.
C. 12 cm.
D. 22 cm.
Theo dõi (0) 1 Trả lời -
ADMICRO


CÓ một tam giác có độ dài ba cạnh lần lượt là 5 cm, 12 cm, 13 cm, bán kính đường tròn ngoại tiếp tam giác đó là bằng
bởi Tran Chau
 11/07/2021
11/07/2021
A. \(\dfrac{5}{2}cm.\)
B. \(5\,cm.\)
C. \(\dfrac{{13}}{2}\,cm.\)
D. \(13\,cm.\)
Theo dõi (0) 1 Trả lời -


Cho hình nón có bán kính đáy là bằng 3m, diện tích toàn phần bằng \(24\pi \,\,{m^2}\). Tính thể tích của hình nón.
bởi Đào Lê Hương Quỳnh
 12/07/2021
12/07/2021
Cho hình nón có bán kính đáy là bằng 3m, diện tích toàn phần bằng \(24\pi \,\,{m^2}\). Tính thể tích của hình nón.
Theo dõi (0) 1 Trả lời -


Cho một tam giác vuông có chu vi bằng 24 cm. Độ dài hai cạnh góc vuông hơn kém nhau 2 cm. Tính diện tích tam giác vuông đó.
bởi Lê Tấn Thanh
 12/07/2021
12/07/2021
Cho một tam giác vuông có chu vi bằng 24 cm. Độ dài hai cạnh góc vuông hơn kém nhau 2 cm. Tính diện tích tam giác vuông đó.
Theo dõi (0) 1 Trả lời -


Cho tam giác đều \(ABC\) có cạnh bằng \(a.\) Hai điểm \(M,\;N\) lần lượt di động trên hai đoạn thẳng \(AB,\;\;AC\) sao cho \(\dfrac{{AM}}{{MB}} + \dfrac{{AN}}{{NC}} = 1.\) Đặt \(AM = x\) và \(AN = y.\) Chứng minh: \(MN = a - x - y.\)
bởi can chu
 11/07/2021
11/07/2021
Cho tam giác đều \(ABC\) có cạnh bằng \(a.\) Hai điểm \(M,\;N\) lần lượt di động trên hai đoạn thẳng \(AB,\;\;AC\) sao cho \(\dfrac{{AM}}{{MB}} + \dfrac{{AN}}{{NC}} = 1.\) Đặt \(AM = x\) và \(AN = y.\) Chứng minh: \(MN = a - x - y.\)\(\(MN = a - x - y.\)\)
Theo dõi (0) 1 Trả lời -


Có tam giác đều ABC có đường cao AH. Trên cạnh BC lấy điểm M tùy ý (M không trùng với B, C, H). Gọi P, Q lần lượt là hình chiếu vuông góc vủa M lên AB và AC.
bởi Long lanh
 12/07/2021
12/07/2021
a) Chứng minh tứ giác APMQ nội tiếp được trong đường tròn và xác định tâm O của đường tròn này.
b) Chứng minh \(OH \bot PQ\).
c) Chứng minh \(MP + MQ = AH\).
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng tọa độ \(Oxy\) đường thẳng \(d\) có hệ số góc \(k\) đi qua điểm \(M\left( {1; - 3} \right)\) cắt các trục \(Ox,\;\;Oy\) lần lượt tại \(A\) và \(B.\) Hãy xác định tọa độ các điểm \(A,\;\;B\) theo \(k.\)
bởi Trieu Tien
 12/07/2021
12/07/2021
Trong mặt phẳng tọa độ \(Oxy\) đường thẳng \(d\) có hệ số góc \(k\) đi qua điểm \(M\left( {1; - 3} \right)\) cắt các trục \(Ox,\;\;Oy\) lần lượt tại \(A\) và \(B.\) Hãy xác định tọa độ các điểm \(A,\;\;B\) theo \(k.\)
Theo dõi (0) 1 Trả lời





