Bài tập 43 tr 130 sách GK Toán lớp 9 Tập 2
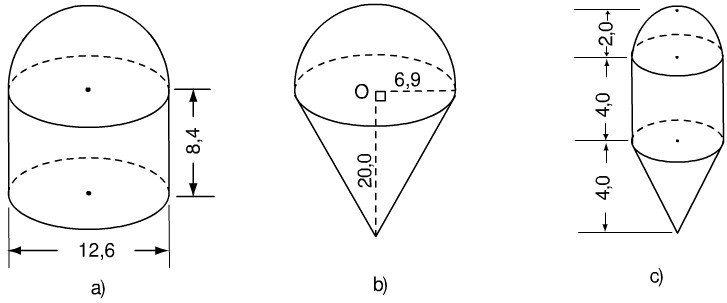
Hãy tính thể tích các hình dưới đây theo kích thước đã cho (h.118) (đơn vị : cm).
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Thể tích hình trụ: \(V=\pi r^2 h.\)
+) Thể tích hình nón: \(V = \dfrac{1}{3}\pi {r^2}h.\)
+) Thể tích hình cầu: \(V = \dfrac{4}{3}\pi {r^3}.\)
Lời giải chi tiết
a) Thể tích hình cần tính gồm một hình trụ có bán kính đáy \(R=12,6:2=6,3,\) chiều cao \(h=8,4\) và nửa hình cầu có bán kính \(R=12,6:2=6,3.\)
Thể tích hình trụ: \(V_1=\pi R^2 h=\pi.6,3^2.8,4=333,4 \pi \, cm^3.\)
Thể tích nửa hình cầu: \(V_2=\dfrac{1}{2}.\dfrac{4}{3}\pi R^3=\dfrac{2}{3}.\pi .6,3^3=166,7\pi \, cm^3.\)
\(\Rightarrow V=V_1+V_2=333,4 \pi +166,7\pi= 500,1 \pi \, cm^3.\)
b) Thể tích hình cần tính gồm một hình nón có bán kính đáy \(R=6,9,\) chiều cao \(h=20\) và nửa hình cầu có bán kính \(R=6,9.\)
Thể tích hình nón: \(V_1=\dfrac{1}{3}.\pi R^2 h=\dfrac{1}{3}.\pi.6,9^2.20=317,4 \pi \, cm^3.\)
Thể tích nửa hình cầu: \(V_2=\dfrac{1}{2}.\dfrac{4}{3}\pi R^3=\dfrac{2}{3}.\pi .6,9^3=219\pi \, cm^3.\)
\(\Rightarrow V=V_1+V_2=317,4 \pi +219\pi= 536,4 \pi \, cm^3.\)
c) Thể tích hình cần tính gồm một hình nón có bán kính đáy \(R=2,\) chiều cao \(h=4\); hình trụ có bán kính đáy \(R=2,\) chiều cao \(h=4\) và nửa hình cầu có bán kính \(R=2.\)
Thể tích hình nón: \(V_1=\dfrac{1}{3}.\pi R^2 h=\dfrac{1}{3}.\pi.2^2.4=\dfrac{16}{3} \pi \, cm^3.\)
Thể tích hình trụ: \(V_2=\pi R^2 h=\pi.2^2.4=16 \pi \, cm^3.\)
Thể tích nửa hình cầu: \(V_3=\dfrac{1}{2}.\dfrac{4}{3}\pi R^3=\dfrac{2}{3}.\pi .2^3=\dfrac{16}{3} \pi \, cm^3.\)
\(\Rightarrow V=V_1+V_2+V_3=\dfrac{16}{3} \pi +16\pi+\dfrac{16}{3} \pi \)\(= \dfrac{80}{3} \pi \, cm^3.\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 41 trang 129 SGK Toán 9 Tập 2
Bài tập 42 trang 130 SGK Toán 9 Tập 2
Bài tập 44 trang 130 SGK Toán 9 Tập 2
Bài tập 42 trang 174 SBT Toán 9 Tập 2
Bài tập 43 trang 174 SBT Toán 9 Tập 2
Bài tập 44 trang 174 SBT Toán 9 Tập 2
Bài tập 45 trang 174 SBT Toán 9 Tập 2
Bài tập 46 trang 175 SBT Toán 9 Tập 2
Bài tập 47 trang 175 SBT Toán 9 Tập 2
Bài tập 48 trang 175 SBT Toán 9 Tập 2
Bài tập 49 trang 175 SBT Toán 9 Tập 2
Bài tập IV.1 trang 176 SBT Toán 9 Tập 2
Bài tập IV.2 trang 176 SBT Toán 9 Tập 2
Bài tập IV.3 trang 176 SBT Toán 9 Tập 2
Bài tập IV.4 trang 177 SBT Toán 9 Tập 2
-


Có cạnh huyền của một tam giác vuông bằng 17 cm. Hai cạnh góc vuông có độ dài hơn kém nhau 7 cm. Tính diện tích của tam giác vuông đó.
bởi Nguyễn Vân
 12/07/2021
12/07/2021
Có cạnh huyền của một tam giác vuông bằng 17 cm. Hai cạnh góc vuông có độ dài hơn kém nhau 7 cm. Tính diện tích của tam giác vuông đó.
Theo dõi (0) 1 Trả lời -


Cầu vòm là một dạng cầu đẹp bởi hình dáng cầu được uốn lượn theo một cung tròn tạo sự hài hòa trong thiết kế cảnh quan, đặc biệt là các khu đô thị có dòng sông chảy qua, tạo được một điểm nhấn của công trình giao thông hiện đại. Một chiếc cầu vòm được thiết kế như hình vẽ bên, vòm cầu là một cung tròn AMB. Độ dài đoạn AB bằng 30m, khoảng cách từ vị trí cao nhất ở giữa vòm cầu so với sàn mặt cầu là đoạn MK có độ dài 5m. Hãy tính chiều dài vòm cầu.
bởi Lê Minh Hải
 11/07/2021
11/07/2021
Cầu vòm là một dạng cầu đẹp bởi hình dáng cầu được uốn lượn theo một cung tròn tạo sự hài hòa trong thiết kế cảnh quan, đặc biệt là các khu đô thị có dòng sông chảy qua, tạo được một điểm nhấn của công trình giao thông hiện đại. Một chiếc cầu vòm được thiết kế như hình vẽ bên, vòm cầu là một cung tròn AMB. Độ dài đoạn AB bằng 30m, khoảng cách từ vị trí cao nhất ở giữa vòm cầu so với sàn mặt cầu là đoạn MK có độ dài 5m. Hãy tính chiều dài vòm cầu.
Theo dõi (0) 1 Trả lời -


Với tam giác đều ABC nội tiếp trong đường tròn tâm O. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA.
bởi Việt Long
 11/07/2021
11/07/2021
a.Chứng minh tứ giác BMON nội tiếp được đường tròn.
b.Kéo dài AN cắt đường tròn (O) tại G (khác A). Chứng minh ON = NG.
b.PN cắt cung nhỏ BG của đường tròn (O) tại điểm F. Tính số đo của góc \(\widehat {OFP}\) .
Theo dõi (0) 1 Trả lời -


Cho đường tròn (O) đường kính AB và một dây CD vuông góc với AB tại H (H không trừng với các điểm A, B, O). Gọi M là trung điểm của AD. Hãy chứng minh:
bởi Co Nan
 12/07/2021
12/07/2021
a) Bốn điểm O, M, D, H cùng thuộc một đường tròn.
b) MH vuông góc với BC.
Theo dõi (0) 1 Trả lời -
ADMICRO


Có các đường tròn như sau \(\left( {A;3cm} \right);\,\,\left( {B;\;5cm} \right);\,\,\left( {C;2cm} \right)\) đôi một tiếp xúc ngoài với nhau. Chu vi của \(\Delta ABC\) là:
bởi Nguyễn Quang Minh Tú
 11/07/2021
11/07/2021
A. 20cm
B. \(10\sqrt 2 cm\)
C. 10cm
D. \(10\sqrt 3 cm\)
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(BH = 3,2cm;\;\;BC = 5cm\) thì độ dài \(AB\) là bằng bao nhiêu?
bởi Nguyễn Thủy
 11/07/2021
11/07/2021
A. \(8cm\) B. -\(16cm\)
C. \(1,8cm\) D. \(4cm\)
Theo dõi (0) 1 Trả lời -


A. \(36\pi c{m^2}\)
B. \(12\pi c{m^2}\)
C. \(216\pi c{m^2}\)
D. \(72\pi c{m^2}\)
Theo dõi (0) 1 Trả lời -


Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AC\), có \(\widehat {BAC} = {60^0}\) (hình vẽ). Khi đó số đo của \(\widehat {ADB}\) là bằng:
bởi Thanh Thanh
 11/07/2021
11/07/2021
A. \({45^0}\) B. \({60^0}\)
C. \({40^0}\) D. \({30^0}\).
Theo dõi (0) 1 Trả lời -


Cho hai đường tròn sau \(\left( {O;\;4cm} \right)\) và đường tròn \(\left( {I;\;2cm} \right),\) biết \(OI = 6cm.\) Số tiếp tuyến chung của hai đường tròn đó là:
bởi Quynh Anh
 12/07/2021
12/07/2021
A. 4 B. 3
C. 2 D. 1
Theo dõi (0) 1 Trả lời -


Cho tam giác \(ABC\) vuông tại \(C.\) Biết \(\sin B = \dfrac{1}{3},\) khi đó \(\tan A\) là bằng:
bởi Hoàng My
 11/07/2021
11/07/2021
A. \(\dfrac{{2\sqrt 2 }}{3}\)
B. \(3\)
C. \(2\sqrt 2 \)
D. \(\dfrac{1}{{2\sqrt 2 }}\)
Theo dõi (0) 1 Trả lời


