Bài tập 3.7 trang 102 SBT Hình học 12

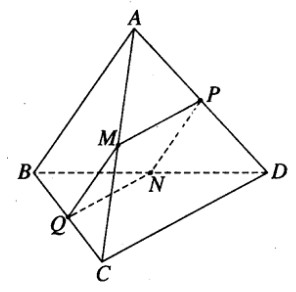
a) Ta có MPNQ là hình bình hành vì \(\overrightarrow {MP}  = \overrightarrow {QN}  = \frac{1}{2}\overrightarrow {CD} \) và \(\overrightarrow {MQ}  = \overrightarrow {PN}  = \frac{1}{2}\overrightarrow {AB} \).

Do đó \(\overrightarrow {MN}  = \overrightarrow {MQ}  + \overrightarrow {MP}  = \frac{{\overrightarrow {AB} }}{2} + \frac{{\overrightarrow {CD} }}{2}\) hay \(2\overrightarrow {MN}  = \overrightarrow {AB}  + \overrightarrow {CD} \)        (1)

Mặt khác \(\overrightarrow {AB}  = \overrightarrow {AD}  + \overrightarrow {DB} \)

              \(\overrightarrow {CD}  = \overrightarrow {CB}  + \overrightarrow {BD} \)

Nên \(\overrightarrow {AB}  + \overrightarrow {CD}  = \overrightarrow {AD}  + \overrightarrow {CB} \)            (2)

Vì \(\overrightarrow {DB}  =  - \overrightarrow {BD} \)

Từ (1) và (2) ta có: \(\overrightarrow {AB}  + \overrightarrow {CD}  = \overrightarrow {AD}  + \overrightarrow {CB}  = 2\overrightarrow {MN} \) là đẳng thức cần chứng minh.

b) Ta có: \(\overrightarrow {PQ}  = \overrightarrow {MQ}  - \overrightarrow {MP}  = \frac{{\overrightarrow {AB} }}{2} - \frac{{\overrightarrow {CD} }}{2}\)

Do đó: \(2\overrightarrow {PQ}  = \overrightarrow {AB}  - \overrightarrow {CD} \)         (3)

Mặt khác: \(\overrightarrow {AB}  = \overrightarrow {AC}  + \overrightarrow {CB} \) 

               \(\overrightarrow {CD}  = \overrightarrow {BD}  - \overrightarrow {BC} \) 

Nên \(\overrightarrow {AB}  - \overrightarrow {CD}  = \overrightarrow {AC}  - \overrightarrow {BD} \)             (4)

Vì \(\overrightarrow {CB}  - ( - \overrightarrow {BC} ) = \vec 0\)

Từ (3) và (4) ta suy ra \(\overrightarrow {AB}  - \overrightarrow {CD}  = \overrightarrow {AC}  - \overrightarrow {BD}  = 2\overrightarrow {PQ} \) là đẳng thức cần chứng minh.

-- Mod Toán 12 HỌC247