Bài tập 2 trang 81 SGK Hình học 12 NC
Cho vecto \(\overrightarrow u \) tùy ý khác \(\overrightarrow 0 \). Chứng minh \({\cos ^2}(\vec u,\vec i) + {\cos ^2}(\vec u,\vec j) + {\cos ^2}(\vec u,\vec k) = 1\)
Hướng dẫn giải chi tiết
Giả sử \(\overrightarrow u = \left( {x;y;z} \right)\)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
cos(\vec u,\vec i) = \frac{{\vec u.\vec i}}{{|\vec u||\vec i|}} = \frac{x}{{\sqrt {{x^2} + {y^2} + {z^2}} }}\\
u \Rightarrow {\cos ^2}(\vec u,\vec i) = \frac{{{x^2}}}{{{x^2} + {y^2} + {z^2}}}
\end{array}\\
\begin{array}{l}
{\cos ^2}(\vec u,\vec j) = \frac{{{y^2}}}{{{x^2} + {y^2} + {z^2}}};\\
{\cos ^2}(\vec u,\vec k) = \frac{{{z^2}}}{{{x^2} + {y^2} + {z^2}}}
\end{array}
\end{array}\)
Vậy
\(\begin{array}{l}
{\cos ^2}(\vec u,\vec i) + {\cos ^2}(\vec u,\vec j) + {\cos ^2}(\vec u,\vec k)\\
= \frac{{{x^2} + {y^2} + {z^2}}}{{{x^2} + {y^2} + {z^2}}} = 1
\end{array}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.16 trang 103 SBT Hình học 12
Bài tập 1 trang 81 SGK Hình học 12 NC
Bài tập 3 trang 81 SGK Hình học 12 NC
Bài tập 4 trang 81 SGK Hình học 12 NC
Bài tập 5 trang 81 SGK Hình học 12 NC
Bài tập 6 trang 81 SGK Hình học 12 NC
Bài tập 7 trang 81 SGK Hình học 12 NC
Bài tập 8 trang 81 SGK Hình học 12 NC
Bài tập 9 trang 81 SGK Hình học 12 NC
Bài tập 10 trang 81 SGK Hình học 12 NC
Bài tập 11 trang 81 SGK Hình học 12 NC
Bài tập 12 trang 82 SGK Hình học 12 NC
-


Tìm vectơ OE thoả 3 điều kiện biết vectơ OA(-3,0,4),OB(5,-2,-14).
bởi Phương Nghi Nguyễn Võ
 04/01/2020
04/01/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm vecto a2*( vectob*vectoc) biết vecto a = ( 1;-1;1) vecto b= (4;0;-1) vecto c = (3;2;-1)
bởi Thuý Hằng
 02/01/2020
Giải hộ e vs ạTheo dõi (1) 5 Trả lời
02/01/2020
Giải hộ e vs ạTheo dõi (1) 5 Trả lời -

 Câu c của bài
Câu c của bài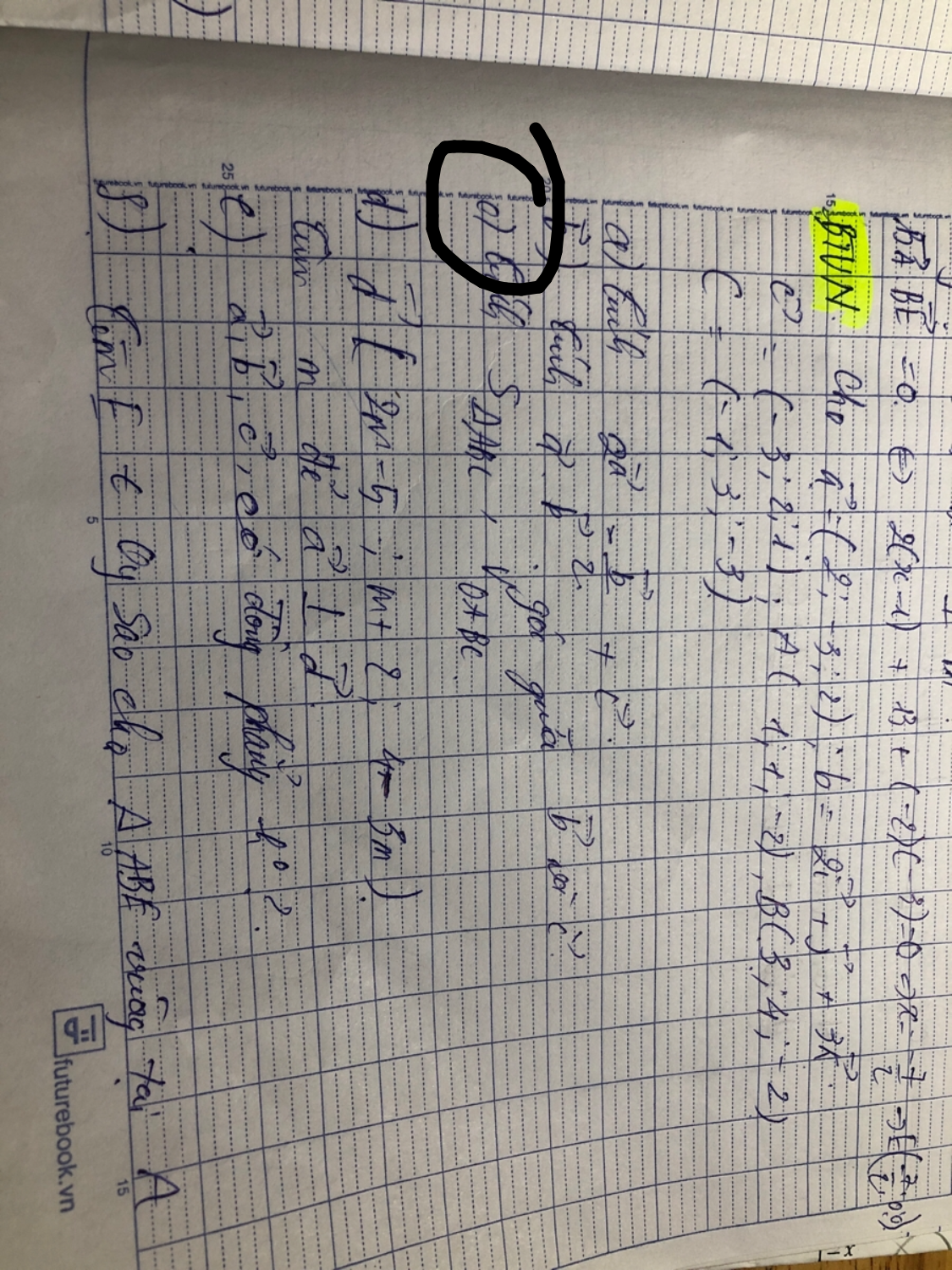 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


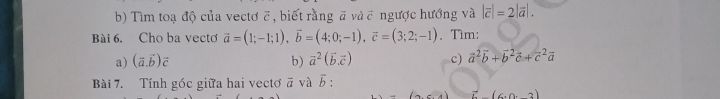 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Tìm tọa độ trọng tâm G của tam giác A’B’C biết hình hộp ABCD.A’B’C’D’ có A(0;0;0); B(3;0;0); D(0;3;0); D’(0;3;-3)
bởi Huyn Anh
 26/12/2019
Cách giải cho bài toán này ạTheo dõi (0) 0 Trả lời
26/12/2019
Cách giải cho bài toán này ạTheo dõi (0) 0 Trả lời -

 Cho hình hộp ABCD.A’B’C’D’, biết A(1;0;1),B'(2;1;2),D'(1;−1;1),C(4;5;−5).Tìm tọa độ đỉnh A’ ?Theo dõi (0) 0 Trả lời
Cho hình hộp ABCD.A’B’C’D’, biết A(1;0;1),B'(2;1;2),D'(1;−1;1),C(4;5;−5).Tìm tọa độ đỉnh A’ ?Theo dõi (0) 0 Trả lời -


 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Diện tích OAB là nhỏ nhất khi K bằng bao nhiêu biết đường thẳng đi qua điểm M(1;3) và có hệ số góc K?
bởi Yến Nhi
 18/12/2019
Toán số 12Theo dõi (0) 2 Trả lời
18/12/2019
Toán số 12Theo dõi (0) 2 Trả lời


