PhαΚßn hΤΑαΜ¦ng dαΚΪn giαΚΘi bΟ†i tαΚ≠p ToΟΓn 11 ChΤΑΤΓng 1 BΟ†i 3 MαΜôt sαΜë phΤΑΤΓng trΟ§nh lΤΑαΜΘng gΟΓc thΤΑαΜùng gαΚΖp sαΚΫ giΟΚp cΟΓc em nαΚ·m ΡëΤΑαΜΘc phΤΑΤΓng phΟΓp vΟ† rΟ®n luyαΜ΅n kΡ© nΡÉng cΟΓc giαΚΘi bΟ†i tαΚ≠p tαΜΪ SGK ΡêαΚΓi sαΜë vΟ† GiαΚΘi tΟ≠ch 11 CΤΓ bαΚΘn-NΟΔng cao.
-
BΟ†i tαΚ≠p 1 trang 36 SGK ΡêαΚΓi sαΜë & GiαΚΘi tΟ≠ch 11
GiαΚΘi phΤΑΤΓng trΟ§nh: \(\small sin^2x - sinx = 0\)
-
BΟ†i tαΚ≠p 2 trang 36 SGK ΡêαΚΓi sαΜë & GiαΚΘi tΟ≠ch 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \(\small 2cos^2x - 3cosx + 1 = 0\);
b) \(\small 2sin2x + \sqrt{2}sin4x = 0\).
-
BΟ†i tαΚ≠p 3 trang 37 SGK ΡêαΚΓi sαΜë & GiαΚΘi tΟ≠ch 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \(sin^2(\frac{x}{2}) - 2cos(\frac{x}{2}) + 2 = 0\);
b) \(\small 8cos^2x + 2sinx - 7 = 0\);
c) \(\small 2tan^2x + 3tanx + 1 = 0\);
d) \(\small tanx -2cotx + 1 = 0\).
-
BΟ†i tαΚ≠p 4 trang 37 SGK ΡêαΚΓi sαΜë & GiαΚΘi tΟ≠ch 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \(\small 2sin^ 2x + sinxcosx - 3cos^2x = 0\)
b) \(\small 3sin^2x - 4sinxcosx + 5cos^2x = 2\)
c) \(\small 3sin^2x - sin2x + 2cos^2x = \frac{1}{2}\)
d) \(\small 2cos^2x -3\sqrt{3}sin2x -4sin^2x = -4\)
- VIDEOYOMEDIA
-
BΟ†i tαΚ≠p 5 trang 37 SGK ΡêαΚΓi sαΜë & GiαΚΘi tΟ≠ch 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \(\small cosx - \sqrt{3}sinx = \sqrt{2}\)
b) \(\small 3sin3x - 4cos3x = 5\)
c) \(\small 2sin2x + 2cos2x -\sqrt{2} = 0\)
d) \(\small 5cos2x + 12sin2x - 13 = 0\)
-
BΟ†i tαΚ≠p 6 trang 37 SGK ΡêαΚΓi sαΜë & GiαΚΘi tΟ≠ch 11
GiαΚΘi phΤΑΤΓng trΟ§nh:
a. \(\small tan(2x + 1) tan(3x - 1) = 1\)
b. \(\small tanx + tan(x + \frac{\pi }{4}) = 1\)
-
BΟ†i tαΚ≠p 1.25 trang 37 SBT ToΟΓn 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau
a) cos2xβà£sinxβà£1 = 0
b) cosxcos2x = 1+sinxsin2x
c) 4sinx.cosx.cos2x = βà£1
d) tanx = 3cotx
-
BΟ†i tαΚ≠p 1.26 trang 37 SBT ToΟΓn 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh
a) 3cos2xβà£2sinx+2 = 0
b) 5sin2x+3cosx+3 = 0
c) sin6x+cos6x = 4cos22x
d) \( - \frac{1}{4} + {\sin ^2}x = {\cos ^4}x\)
-
BΟ†i tαΚ≠p 1.27 trang 37 SBT ToΟΓn 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau
a) 2tanxβà£3cotxβà£2 = 0
b) cos2x = 3sin2x+3
c) cotxβà£cot2x = tanx+1
-
BΟ†i tαΚ≠p 1.28 trang 38 SBT ToΟΓn 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau
a) cos2x+2sinxcosx+5sin2x = 2
b) 3cos2xβà£2sin2x+sin2x = 1
c) 4cos2xβà£3sinxcosx+3sin2x = 1
-
BΟ†i tαΚ≠p 1.29 trang 38 SBT ToΟΓn 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau
a) 2cosxβà£sinx = 2
b) sin5x+cos5x = βà£1
c) 8cos4xβà£4cos2x+sin4xβà£4 = 0
d) \({\sin ^6}x + {\cos ^6}x + \frac{1}{2}\sin 4x = 0\)
-
BΟ†i tαΚ≠p 1.30 trang 38 SBT ToΟΓn 11
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau
a) 1+sinxβà£cosxβà£sin2x + 2cos2x = 0
b) \(\sin x - \frac{1}{{\sin x}} = {\sin ^2}x - \frac{1}{{{{\sin }^2}x}}\)
c) cosxtan3x = sin5x
d) 2tan2x+3tanx2cot2x+3cotx+2 = 0
-
BΟ†i tαΚ≠p 1.31 trang 38 SBT ToΟΓn 11
GiαΚΘi phΤΑΤΓng trΟ§nh \(\cot x - \tan x + 4\sin 2x = \frac{2}{{\sin 2x}}\)
-
BΟ†i tαΚ≠p 1.32 trang 38 SBT ToΟΓn 11
NghiαΜ΅m cαΜßa phΤΑΤΓng trΟ§nh \(3\cot x - \sqrt 3 = 0\) lΟ†
A. \(\frac{\pi }{6} + k\pi \left( {k \in Z} \right)\)
B. \(\frac{\pi }{3} + k\pi \left( {k \in Z} \right)\)
C. \(\frac{\pi }{4} + k\pi \left( {k \in Z} \right)\)
D. \(\frac{\pi }{6} + k\pi \left( {k 2\in Z} \right)\)
-
BΟ†i tαΚ≠p 1.33 trang 38 SBT ToΟΓn 11
NghiαΜ΅m cαΜßa phΤΑΤΓng trΟ§nh sau sin4xβà£cos4x = 0 lΟ†
A. \(\frac{\pi }{2} + k\pi ,k \in Z\)
B. \(\frac{\pi }{3} + k\pi ,k \in Z\)
C. \(\frac{\pi }{4} + k\frac{\pi }{2},k \in Z\)
D. \(\frac{\pi }{6} + k\pi ,k \in Z\)
-
BΟ†i tαΚ≠p 1.34 trang 38 SBT ToΟΓn 11
Cho phΤΑΤΓng trΟ§nh \(4{\cos ^2}2x + 16\sin x\cos x - 7 = 0\) (1)
XΟ©t cΟΓc giΟΓ trαΜ΄ :
(I) \(\frac{\pi }{{12}} + k\pi \)
(II) \(\frac{{5\pi }}{{12}} + k\pi \left( {k \in Z} \right)\)
(III) \(\frac{\pi }{{12}} + k\pi \)
Trong cΟΓc giΟΓ trαΜ΄ trΟΣn giΟΓ trαΜ΄ nΟ†o lΟ† nghiαΜ΅m cαΜßa phΤΑΤΓng trΟ§nh (1) ?
A. ChαΜâ (I)
B. ChαΜâ (II)
C. ChαΜâ (III)
D. (II) vφ (III)
-
BΟ†i tαΚ≠p 1.35 trang 39 SBT ToΟΓn 11
NghiαΜ΅m cαΜßa phΤΑΤΓng trΟ§nh cosx.cos7x = cos3x.cos5x lΟ†
A. \({\frac{\pi }{6} + k\pi ,k \in Z}\)
B. \({-\frac{\pi }{6} + k2\pi ,k \in Z}\)
C. \({k\frac{\pi }{4},k \in Z}\)
D. \({k\frac{\pi }{3},k \in Z}\)
-
BΟ†i tαΚ≠p 1.38 trang 39 SBT ToΟΓn 11
Cho phΤΑΤΓng trΟ§nh \(\sqrt 3 \cos x + \sin x = 2{\rm{(*)}}\)
XΟ©t cΟΓc giΟΓ trαΜ΄
(I) \(\frac{\pi }{2} + k2\pi \)
(II) \(\frac{\pi }{3} + k2\pi \)
(III) \(\frac{\pi }{6} + k2\pi \)
(\(k\in Z\))
Trong cΟΓc giΟΓ trαΜ΄ trΟΣn, giΟΓ trαΜ΄ nΟ†o Ο† nghiαΜ΅m cαΜßa phΤΑΤΓng trΟ§nh (*)?
A. ChαΜâ (I)
B. ChαΜâ (II)
C. ChαΜâ (III)
D. (I) vφ (III)
-
BΟ†i tαΚ≠p 1.36 trang 39 SBT ToΟΓn 11
NghiαΜ΅m cαΜßa phΤΑΤΓng trΟ§nh 3tan2x+6cotx = βà£tanx lΟ†
A. \(k\frac{\pi }{4},k \in Z\)
B. \( \pm \frac{\pi }{3} + k\pi ,k \in Z\)
C. \(\frac{\pi }{6} + k\pi ,k \in Z\)
D. \(k\frac{\pi }{2},k \in Z\)
-
BΟ†i tαΚ≠p 1.37 trang 39 SBT ToΟΓn 11
NghiαΜ΅m cαΜßa phΤΑΤΓng trΟ§nh 2sinx = 3cotx lΟ†
A. \(\frac{\pi }{6} + k2\pi ,k \in Z\)
B. \( \pm \frac{\pi }{3} + k2\pi ,k \in Z\)
C. \(\frac{\pi }{4} + k2\pi ,k \in Z\)
D. \( \pm \frac{\pi }{3} + k2\pi ,k \in Z\)
-
BΟ†i tαΚ≠p 27 trang 41 SGK ToΟΓn 11 NC
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \(2\cos x - \sqrt 3 = 0\)
b) \(\sqrt 3 \tan 3x - 3 = 0\)
c) \(\left( {\sin x + 1} \right)\left( {2\cos 2x - \sqrt 2 } \right) = 0\)
-
BΟ†i tαΚ≠p 28 trang 41 SGK ToΟΓn 11 NC
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \(2{\cos ^2}x - 3\cos x + 1 = 0\)
b) \({\cos ^2}x + \sin x + 1 = 0\)
c) \(\sqrt 3 {\tan ^2}x - \left( {1 + \sqrt 3 } \right)\tan x + 1 = 0\)
-
BΟ†i tαΚ≠p 29 trang 41 SGK ToΟΓn 11 NC
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau trΟΣn khoαΚΘng ΡëΟΘ cho rαΜ™i dΟΙng bαΚΘng sαΜë hoαΚΖc mΟΓy tΟ≠nh bαΜè tΟΚi ΡëαΜÉ tΟ≠nh gαΚßn ΡëΟΚng nghiαΜ΅m cαΜßa chΟΚng (tΟ≠nh chΟ≠nh xΟΓc ΡëαΚΩn hΟ†ng phαΚßn trΡÉm):
a. \(3\cos 2x + 10\sin x + 1 = 0\) trΟΣn \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
b. \(4\cos 2x + 3 = 0\) trΟΣn \(\left( {0;\frac{\pi }{2}} \right)\)
c. \({\cot ^2}x - 3\cot x - 10 = 0\) trΟΣn (0;œÄ)
d. 5βà£3tan3x = 0 trΟΣn \(\left( { - \frac{\pi }{6};\frac{\pi }{6}} \right)\)
-
BΟ†i tαΚ≠p 30 trang 41 SGK ToΟΓn 11 NC
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \(3\cos x + 4\sin x = - 5\)
b) \(2\sin 2x - 2\cos 2x = \sqrt 2 \)
c) \(5\sin 2x - 6{\cos ^2}x = 13\)
-
BΟ†i tαΚ≠p 31 trang 42 SGK ToΟΓn 11 NC
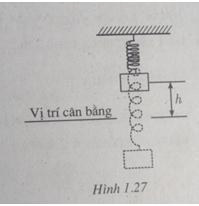
MαΜôt vαΚ≠t nαΚΖng treo bαΜüi mαΜôt chiαΚΩc lΟ≤ xo chuyαΜÉn ΡëαΜông lΟΣn xuαΜëng qua vαΜ΄ trΟ≠ cΟΔn bαΚ±ng. KhoαΚΘng cΟΓch h tαΜΪ vαΚ≠t ΡëΟ≥ ΡëαΚΩn vαΜ΄ trΟ≠ cΟΔn bαΚ±ng αΜü thαΜùi ΡëiαΜÉm t giΟΔy ΡëΤΑαΜΘc tΟ≠nh theo cΟ¥ng thαΜ©c h = |d| trong ΡëΟ≥ d = 5sin6tβÄ™4cos6t vαΜ¦i d ΡëΤΑαΜΘc tΟ≠nh bαΚ±ng xentimet, ta quy ΤΑαΜ¦c rαΚ±ng d > 0 khi vαΚ≠t αΜü phΟ≠a trΟΣn vαΜ΄ trΟ≠ cΟΔn bαΚ±ng, d < 0 khi vαΚ≠t αΜü phΟ≠a dΤΑαΜ¦i vαΜ΄ trΟ≠ cΟΔn bαΚ±ng. HαΜèi:
a. αΜû thαΜùi ΡëiαΜÉm nΟ†o trong 1 giΟΔy ΡëαΚßu tiΟΣn, vαΚ≠t αΜü vαΜ΄ trΟ≠ cΟΔn bαΚ±ng?
b. αΜû thαΜùi ΡëiαΜÉm nΟ†o trong 1 giΟΔy ΡëαΚßu tiΟΣn, vαΚ≠t αΜü xa vαΜ΄ trΟ≠ cΟΔn bαΚ±ng nhαΚΞt?
(TΟ≠nh chΟ≠nh xΟΓc ΡëαΚΩn \(\frac{1}{{100}}\) giΟΔy).
-
BΟ†i tαΚ≠p 32 trang 42 SGK ToΟΓn 11 NC
TΟ§m giΟΓ trαΜ΄ lαΜ¦n nhαΚΞt vΟ† giΟΓ trαΜ΄ nhαΜè nhαΚΞt cαΜßa mαΜ½i biαΜÉu thαΜ©c sau:
a. asinx+bcosx (a vΟ† b lΟ† hαΚ±ng sαΜë, a2+b2 β↠0) ;
b. sin2x+sinxcosx+3cos2x;
c. Asin2x+Bsinxcosx+Ccos2x (A, B vΟ† C lΟ† hαΚ±ng sαΜë).
-
BΟ†i tαΚ≠p 33 trang 42 SGK ToΟΓn 11 NC
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a. \(2{\sin ^2}x + 3\sqrt 3 \sin x\cos x - {\cos ^2}x = 4\)
b. \(3{\sin ^2}x + 4\sin 2x + \left( {8\sqrt 3 - 9} \right){\cos ^2}x = 0\)
c. \({\sin ^2}x + \sin 2x - 2{\cos ^2}x = \frac{1}{2}\)
-
BΟ†i tαΚ≠p 34 trang 42 SGK ToΟΓn 11 NC
SαΜ≠ dαΜΞng cΟ¥ng thαΜ©c biαΚΩn ΡëαΜïi tαΜïng thΟ†nh tΟ≠ch hoαΚΖc tΟ≠ch thΟ†nh tαΜïng ΡëαΜÉ giαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \(\cos x\cos 5x = \cos 2x\cos 4x\)
b) \(\cos 5x\sin 4x = \cos 3x\sin 2x\)
c) \(\sin 2x + \sin 4x = \sin 6x\)
d) \(\sin x + \sin 2x = \cos x + \cos 2x\)
-
BΟ†i tαΚ≠p 35 trang 42 SGK ToΟΓn 11 NC
DΟΙng cΟ¥ng thαΜ©c hαΚΓ bαΚ≠c ΡëαΜÉ giαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \({\sin ^2}4x + {\sin ^2}3x = {\sin ^2}2x + {\sin ^2}x\)
b) \({\cos ^2}x + {\cos ^2}2x + {\cos ^2}3x + {\cos ^2}4x = 2\)
-
BΟ†i tαΚ≠p 36 trang 42 SGK ToΟΓn 11 NC
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a. \(\tan \frac{x}{2} = \tan x\)
b. \(\tan \left( {2x + {{10}^0}} \right) + \cot x = 0\)
c. \(\left( {1 - \tan x} \right)\left( {1 + \sin 2x} \right) = 1 + \tan x\)
d. tanx+tan2x = sin3xcosx
e. tanx+cot2x = 2cot4x
-
BΟ†i tαΚ≠p 37 trang 46 SGK ToΟΓn 11 NC
MΟΙa xuΟΔn αΜü HαΜôi Lim (tαΜânh BαΚ·c Ninh) thΤΑαΜùng cΟ≥ trΟ≤ chΤΓi Ρëu. Khi ngΤΑαΜùi chΤΓi Ρëu nhΟΚn ΡëαΜ¹u, cΟΔy Ρëu sαΚΫ ΡëΤΑa ngΤΑαΜùi chΤΓi Ρëu dao ΡëαΜông qua lαΚΓi vαΜ΄ trΟ≠ cΟΔn bαΚ±ng. NghiΟΣn cαΜ©u trΟ≤ chΤΓi nΟ†y, ngΤΑαΜùi ta thαΚΞy khoαΚΘng cΟΓch h (tΟ≠nh bαΚ±ng mΟ©t) tαΜΪ ngΤΑαΜùi chΤΓi Ρëu ΡëαΚΩn vαΜ΄ trΟ≠ cΟΔn bαΚ±ng (h. 1.32) ΡëΤΑαΜΘc biαΜÉu diαΜÖn qua thαΜùi gian t (t βâΞ 0 vΟ† ΡëΤΑαΜΘc tΟ≠nh bαΚ±ng giΟΔy) bαΜüi hαΜ΅ thαΜ©c h = |d| vαΜ¦i \(d = 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]\), trong ΡëΟ≥ ta quy ΤΑαΜ¦c rαΚ±ng d > 0 khi vαΜ΄ trΟ≠ cΟΔn bαΚ±ng αΜü vαΜ¹ phΟ≠a sau lΤΑng ngΤΑαΜùi chΤΓi Ρëu vΟ† d < 0 trong trΤΑαΜùng hαΜΘp trΟΓi lαΚΓi.
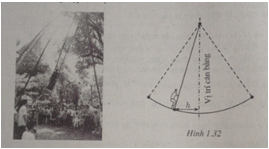
a. TΟ§m cΟΓc thαΜùi ΡëiαΜÉm trong vΟ≤ng 2 giΟΔy ΡëαΚßu tiΟΣn mΟ† ngΤΑαΜùi chΤΓi Ρëu αΜü xa vαΜ΄ trΟ≠ cΟΔn bαΚ±ng nhαΚΞt.
b. TΟ§m cΟΓc thαΜùi ΡëiαΜÉm trong vΟ≤ng 2 giΟΔy ΡëαΚßu tiΟΣn mΟ† ngΤΑαΜùi chΤΓi Ρëu cΟΓch vαΜ΄ trΟ≠ cΟΔn bαΚ±ng 2 mΟ©t (tΟ≠nh chΟ≠nh xΟΓc ΡëαΚΩn \(\frac{1}{{100}}\) giΟΔy).
-
BΟ†i tαΚ≠p 38 trang 46 SGK ToΟΓn 11 NC
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \({\cos ^2}x - 3{\sin ^2}x = 0\)
b) \({\left( {\tan x + \cot x} \right)^2} - \left( {\tan x + \cot x} \right) = 2\)
c) \(\sin x + {\sin ^2}\frac{x}{2} = 0,5\)
-
BΟ†i tαΚ≠p 39 trang 46 SGK ToΟΓn 11
ChαΜ©ng minh rαΚ±ng cΟΓc phΤΑΤΓng trΟ§nh sau ΡëΟΔy vΟ¥ nghiαΜ΅m:
a. sinxβÄ™2cosx = 3
b. 5sin2x+sinx+cosx+6 = 0
HΤΑαΜ¦ng dαΚΪn b. ΡêαΚΖt sinx+cosx = t
-
BΟ†i tαΚ≠p 40 trang 46 SGK ToΟΓn 11 NC
TΟ§m cΟΓc nghiαΜ΅m cαΜßa mαΜ½i phΤΑΤΓng trΟ§nh sau trong khoαΚΘng ΡëΟΘ cho (khi cαΚßn tΟ≠nh gαΚßn ΡëΟΚng thΟ§ tΟ≠nh chΟ≠nh xΟΓc ΡëαΚΩn \(\frac{1}{{10}}\) giΟΔy)
a. \(2{\sin ^2}x - 3\cos x = 2,{0^0} \le x \le {360^0}\)
b. \(\tan x + 2\cot x = 3,\,\,{180^0} \le x \le {360^0}\)
-
BΟ†i tαΚ≠p 41 trang 47 SGK ToΟΓn 11 NC
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a. 3sin2xβà£sin2xβà£cos2x = 0
b. 3sin22xβà£sin2xcos2xβà£4cos22x = 2
c. \(2\sin 2x + \left( {3 + \sqrt 3 } \right)\sin x\cos x + \left( {\sqrt 3 - 1} \right)\cos 2x = - 1\)
-
BΟ†i tαΚ≠p 42 trang 47 SGK ToΟΓn 11 NC
GiαΚΘi cΟΓc phΤΑΤΓng trΟ§nh sau:
a) \(\sin x + \sin 2x + \sin 3x = \cos x + \cos 2x + \cos 3x\)
b) \(\sin x = \sqrt 2 \sin 5x - \cos x\)
c) \(\frac{1}{{\sin 2x}} + \frac{1}{{\cos 2x}} = \frac{2}{{\sin 4x}}\)
d) \(\sin x + \cos x = \frac{{\cos 2x}}{{1 - \sin 2x}}\)





