Giải bài 1.34 tr 38 SBT Toán 11
Cho phương trình \(4{\cos ^2}2x + 16\sin x\cos x - 7 = 0\) (1)
Xét các giá trị :
(I) \(\frac{\pi }{{12}} + k\pi \)
(II) \(\frac{{5\pi }}{{12}} + k\pi \left( {k \in Z} \right)\)
(III) \(\frac{\pi }{{12}} + k\pi \)
Trong các giá trị trên giá trị nào là nghiệm của phương trình (1) ?
A. Chỉ (I)
B. Chỉ (II)
C. Chỉ (III)
D. (II) và (III)
Hướng dẫn giải chi tiết
Ta có: \({\rm{(1)}} \Leftrightarrow 4(1 - {\sin ^2}2x) + 8\sin 2x - 7 = 0\)
\(\begin{array}{l}
\Leftrightarrow 4{\sin ^2}2x - 8\sin 2x + 3 = 0\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\sin 2x = \frac{3}{2} > 1\,\,{\rm{(l)}}}\\
{\sin 2x = \frac{1}{2}}
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{2x = \frac{\pi }{6} + k2\pi ,k \in Z}\\
{2x = \pi - (\frac{\pi }{6}) + k2\pi ,k \in Z}
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{{12}} + k\pi ,k \in Z}\\
{x = \frac{{5\pi }}{{12}} + k\pi ,k \in Z}
\end{array}} \right.
\end{array}\)
Đáp án: D.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 1.32 trang 38 SBT Toán 11
Bài tập 1.33 trang 38 SBT Toán 11
Bài tập 1.35 trang 39 SBT Toán 11
Bài tập 1.38 trang 39 SBT Toán 11
Bài tập 1.36 trang 39 SBT Toán 11
Bài tập 1.37 trang 39 SBT Toán 11
Bài tập 27 trang 41 SGK Toán 11 NC
Bài tập 28 trang 41 SGK Toán 11 NC
Bài tập 29 trang 41 SGK Toán 11 NC
Bài tập 30 trang 41 SGK Toán 11 NC
Bài tập 31 trang 42 SGK Toán 11 NC
Bài tập 32 trang 42 SGK Toán 11 NC
Bài tập 33 trang 42 SGK Toán 11 NC
Bài tập 34 trang 42 SGK Toán 11 NC
Bài tập 35 trang 42 SGK Toán 11 NC
Bài tập 36 trang 42 SGK Toán 11 NC
Bài tập 37 trang 46 SGK Toán 11 NC
Bài tập 38 trang 46 SGK Toán 11 NC
Bài tập 39 trang 46 SGK Toán 11
Bài tập 40 trang 46 SGK Toán 11 NC
-


Nếu đặt t=cosx/2 thì phương trình cosx+ cosx/2-1=0 trở thành phương trình nào?
bởi Ngân Nhã
 27/09/2019
27/09/2019
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Giải phương trình căn 3sin2x+cos2x=2cosx-1
bởi Giang Vương Quỳnh
 14/09/2019
Help me ?!!!
14/09/2019
Help me ?!!! Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -

 sinx sin 2x sin 3x ... sin (nx)= n( với n€ N* )Theo dõi (1) 3 Trả lời
sinx sin 2x sin 3x ... sin (nx)= n( với n€ N* )Theo dõi (1) 3 Trả lời -


Giải phương trình sin 3x / cos 3x - 1=0
bởi Nguyễn Thị Thu Thảo
 02/09/2019
02/09/2019
sin 3x / cos 3x - 1=0
Theo dõi (0) 4 Trả lời -
ADMICRO


Giải phương trình (cos(3x+pi/2)+1).sin(x+pi/5)=0
bởi Minh Trần
 24/08/2019
24/08/2019
:
cần lắm cao nhân :V xin cảm ơn
Theo dõi (0) 3 Trả lời -


Tìm m để 2 phương trình sinxcosx + 2sinx - cosx - 2 = 0 và cos2x = m tương đương
bởi Thùy Linh
 06/08/2019
06/08/2019
Tìm các giá trị của m để 2 pt sinxcosx + 2sinx - cosx - 2 = 0 và cos2x = m tương đương
Theo dõi (0) 2 Trả lời -

 Mọi người giúp mik câu này đc k???
Mọi người giúp mik câu này đc k???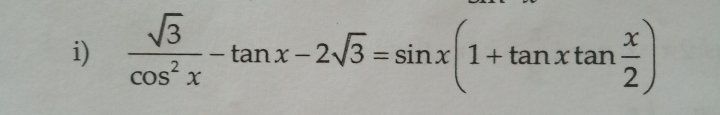 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình tan(pi/6+2x)+2cot(pi/6+2x)
bởi Phương Dung Lê
 02/07/2019
02/07/2019
giải phương trình:
a,tan(
) + 2cot(
) -3 =0
b, sin(
) - cos
=0
Giải giúp mình với ạ!!
Theo dõi (1) 2 Trả lời -


Cho phương trình 2cos^2x +5sinxcosx+6sin2x-m-1=0 số giá trị m thuộc z để phương trình có nghiệm là
Theo dõi (0) 1 Trả lời -


Giải phương trình sin2x+sin4x+sin6x+sin8x=0
bởi Nguyễn Thanh Hoài
 18/10/2018
18/10/2018
sin2x+sin4x+sin6x+sin8x=0
Theo dõi (0) 2 Trả lời -


Giải phương trình 2sinxcosx+cosxcos2x=sinx-2cos2x
bởi Moon Matt
 17/10/2018
17/10/2018
2sinxcosx+cosxcos2x=sinx-2cos2x
Cảm ơn ạ
Theo dõi (0) 1 Trả lời -


Giải phương trình cos 2x-căn 3sin 2x=2cosx
bởi Yến Nhi
 13/10/2018
13/10/2018
cos2x -
=2cosx
Theo dõi (0) 2 Trả lời -


cos (2x - pi\4) - sin2x + pi/3 = 0
Theo dõi (0) 2 Trả lời -


1. giải pt : sin4x + cos3x + cosx = 4 sinx + 2
2. biến đổi, rút gọn : A= 1 + 2cosacosbcosc - ( cos2a + cos2b + cos2c )
Theo dõi (0) 3 Trả lời -


(căn3)cos2x + sin2x + 2sin(2x-pi/6) = 2căn2?
Theo dõi (0) 3 Trả lời







