Giải bài 65 tr 100 sách GK Toán 8 Tập 1
Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
Hướng dẫn giải chi tiết
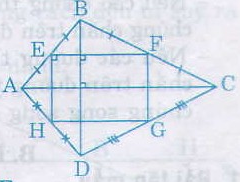
Ta có EB = EA, FB = FC (gt)
Nên EF là đường trung bình của ∆ABC
Do đó EF // AC
HD = HA, GD = GC
Nên HG là đường trung bình của ∆ADC
Do đó HG // AC
Suy ra EF // HG
Tương tự EH // FG
Do đó EFGH là hình bình hành.
EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH hay = 900
Hình bình hành EFGH có \(\widehat{E} = 90^0\) nên là hình chữ nhật.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 63 trang 100 SGK Toán 8 Tập 1
Bài tập 64 trang 100 SGK Toán 8 Tập 1
Bài tập 66 trang 100 SGK Toán 8 Tập 1
Bài tập 106 trang 93 SBT Toán 8 Tập 1
Bài tập 107 trang 93 SBT Toán 8 Tập 1
Bài tập 108 trang 93 SBT Toán 8 Tập 1
Bài tập 109 trang 93 SBT Toán 8 Tập 1
Bài tập 110 trang 93 SBT Toán 8 Tập 1
Bài tập 111 trang 94 SBT Toán 8 Tập 1
Bài tập 112 trang 94 SBT Toán 8 Tập 1
Bài tập 113 trang 94 SBT Toán 8 Tập 1
Bài tập 114 trang 94 SBT Toán 8 Tập 1
Bài tập 115 trang 94 SBT Toán 8 Tập 1
Bài tập 116 trang 94 SBT Toán 8 Tập 1
Bài tập 117 trang 94 SBT Toán 8 Tập 1
Bài tập 118 trang 94 SBT Toán 8 Tập 1
Bài tập 119 trang 94 SBT Toán 8 Tập 1
Bài tập 120 trang 95 SBT Toán 8 Tập 1
Bài tập 121 trang 95 SBT Toán 8 Tập 1
Bài tập 122 trang 95 SBT Toán 8 Tập 1
Bài tập 123 trang 95 SBT Toán 8 Tập 1
Bài tập 9.1 trang 95 SBT Toán 8 Tập 1
-


Chứng minh tứ giác ABCD là hình thoi
bởi Võ Vy
 25/12/2019
25/12/2019
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Chứng minh tứ giác BDCN là hình bình hành
bởi Người Lạ Ơi
 20/12/2019
Cho tam giác ABC vuông tại A. Gọi M,N lần lượt là trung điểm của BC và AC, gọi D là điểm đối xứng với N qua Ma, Chứng minh rằng: tứ giác BDCN là hình bình hànhb, Chứng minh rằng: AD=BNTheo dõi (1) 2 Trả lời
20/12/2019
Cho tam giác ABC vuông tại A. Gọi M,N lần lượt là trung điểm của BC và AC, gọi D là điểm đối xứng với N qua Ma, Chứng minh rằng: tứ giác BDCN là hình bình hànhb, Chứng minh rằng: AD=BNTheo dõi (1) 2 Trả lời -


Chứng minh tứ giác NIBM là hình bình hành
bởi Thanhtam Le
 18/12/2019
Cho hình chữ nhật ABCD gọi E là hình chiếu của C trên BD, gọi M, N, I lần lượt là trung điểm của CE, ED, AB.a) Chứng minh tứ giác NIBM là hình bình hành b) Chứng minh BM vuông góc với NCc) Gọi K là giao điểm của BM với NC, H là hình chiếu của I trên BM. Chứng minh tứ giác IHKN là hình chữ nhậtTheo dõi (1) 4 Trả lời
18/12/2019
Cho hình chữ nhật ABCD gọi E là hình chiếu của C trên BD, gọi M, N, I lần lượt là trung điểm của CE, ED, AB.a) Chứng minh tứ giác NIBM là hình bình hành b) Chứng minh BM vuông góc với NCc) Gọi K là giao điểm của BM với NC, H là hình chiếu của I trên BM. Chứng minh tứ giác IHKN là hình chữ nhậtTheo dõi (1) 4 Trả lời -


Cho tam giac AB nhọn , đường cao BE và CF cắt nhau tại H . Gọi M là trung điểm của BC và I là điểm đối xứng với H qua M
bởi Gia Gia
 19/11/2019
19/11/2019
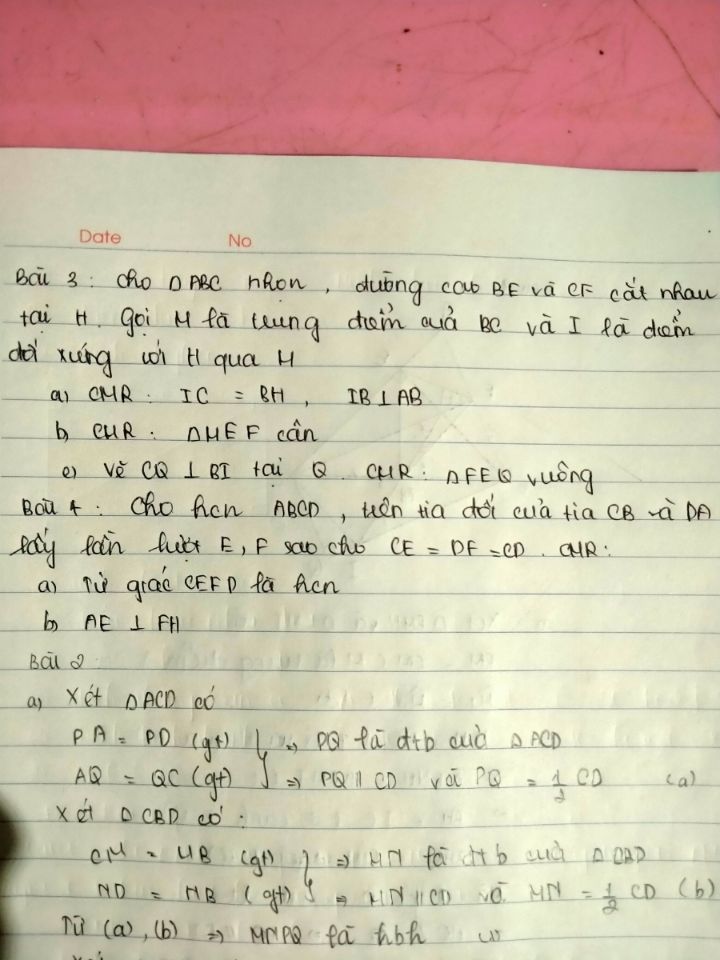 Theo dõi (2) 2 Trả lời
Theo dõi (2) 2 Trả lời -
ADMICRO


Cho tam giác ABC có đường cao AH, M, N lần lượt là trung điểm của AB, AC, BC
bởi Tiên Thủy
 12/11/2019
12/11/2019
 Theo dõi (3) 2 Trả lời
Theo dõi (3) 2 Trả lời -


Cho tam giác ABC cân tại A, đường cao AH,gọi O là trung điểm AB, E đối xứng với H qua O
bởi ThuHien Hien
 10/11/2019
10/11/2019
cho tam giác abc
Theo dõi (0) 5 Trả lời





