Giải bài 64 tr 100 sách GK Toán 8 Tập 1
Cho hình bình hành ABCD. Các tia phân giác cảu các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
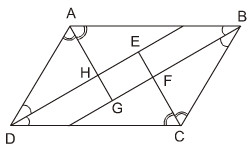
Hướng dẫn giải chi tiết
Theo giả thiết \(ABCD\) là hình bình hành nên \(AD//BC,AB//CD\)
Vì \(AD//BC\) \( \Rightarrow \widehat {DAB} + \widehat {ABC}= {180^0}\) (hai góc trong cùng phía bù nhau)
Vì \(AG\) là tia phân giác \(\widehat {DAB}\) (giả thiết)
\( \Rightarrow \) \(\widehat {BAG}=\widehat {DAH} = \dfrac{1}{2}\widehat {DAB}\) (tính chất tia phân giác)
Vì \(BG\) là tia phân giác \(\widehat {ABC}\) (giả thiết)
\( \Rightarrow \) \(\widehat {ABG} = \dfrac{1}{2}\widehat {ABC}\)
Do đó: \(\widehat {BAG} + \widehat {ABG} = \dfrac{1}{2}\left( {\widehat {DAB} + \widehat {ABC}} \right) \)\(= \dfrac{1}{2}{.180^0} = {90^0}\)
Xét \(\Delta AGB\) có:
\(\widehat {BAG} + \widehat {ABG} = {90^0}\)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác \(AGB\) ta có:
\(\widehat {BAG} + \widehat {ABG} + \widehat {AGB} = {180^0}\)
\( \Rightarrow\widehat {AGB} =180^0- (\widehat {BAG} + \widehat {ABG} )\)\(=180^0-{90^0}=90^0\) (*)
+ Vì \(AB//DC\) \( \Rightarrow \widehat {DAB} + \widehat {ADC}= {180^0}\) (hai góc trong cùng phía bù nhau)
+ Vì \(DE\) là tia phân giác \(\widehat {ADC}\) (giả thiết)
\( \Rightarrow \) \(\widehat {ADH}=\widehat {EDC} = \dfrac{1}{2}\widehat {ADC}\) (tính chất tia phân giác)
Do đó: \(\widehat {DAH} + \widehat {ADH} = \dfrac{1}{2}\left( {\widehat {DAB} + \widehat {ADC}} \right) \)\(= \dfrac{1}{2}{.180^0} = {90^0}\)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác \(ADH\) ta có:
\(\widehat {DAH} + \widehat {ADH} + \widehat {AHD} = {180^0}\)
\( \Rightarrow\widehat {AHD} =180^0- (\widehat {DAH} + \widehat {ADH} )\)\(=180^0-{90^0}=90^0\)
Suy ra \(AH\bot HD\) nên \(\widehat {EHG}=90^0\) (**)
Chứng minh tương tự:
Ta có: \( \widehat {DCB} + \widehat {ADC}= {180^0}\) (hai góc trong cùng phía bù nhau)
Mà \(\widehat{ECD}=\dfrac{1}2\widehat {DCB}\) (do CE là phân giác góc DCB)
Nên \(\widehat {EDC} + \widehat {ECD} = \dfrac{1}{2}\left( {\widehat {ADC} + \widehat {DCB}} \right) \)\(= \dfrac{1}{2}{.180^0} = {90^0}\)
Lại có:
\(\widehat {EDC} + \widehat {ECD} + \widehat {DEC} = {180^0}\) (tổng ba góc trong tam giác DEC)
\( \Rightarrow\widehat {DEC} =180^0- (\widehat {EDC} + \widehat {ECD} )\)\(=180^0-{90^0}=90^0\)
Hay \(\widehat {HEF} = {90^0}\) (***)
Từ (*), (**) và (***) ta thấy tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 62 trang 99 SGK Toán 8 Tập 1
Bài tập 63 trang 100 SGK Toán 8 Tập 1
Bài tập 65 trang 100 SGK Toán 8 Tập 1
Bài tập 66 trang 100 SGK Toán 8 Tập 1
Bài tập 106 trang 93 SBT Toán 8 Tập 1
Bài tập 107 trang 93 SBT Toán 8 Tập 1
Bài tập 108 trang 93 SBT Toán 8 Tập 1
Bài tập 109 trang 93 SBT Toán 8 Tập 1
Bài tập 110 trang 93 SBT Toán 8 Tập 1
Bài tập 111 trang 94 SBT Toán 8 Tập 1
Bài tập 112 trang 94 SBT Toán 8 Tập 1
Bài tập 113 trang 94 SBT Toán 8 Tập 1
Bài tập 114 trang 94 SBT Toán 8 Tập 1
Bài tập 115 trang 94 SBT Toán 8 Tập 1
Bài tập 116 trang 94 SBT Toán 8 Tập 1
Bài tập 117 trang 94 SBT Toán 8 Tập 1
Bài tập 118 trang 94 SBT Toán 8 Tập 1
Bài tập 119 trang 94 SBT Toán 8 Tập 1
Bài tập 120 trang 95 SBT Toán 8 Tập 1
Bài tập 121 trang 95 SBT Toán 8 Tập 1
Bài tập 122 trang 95 SBT Toán 8 Tập 1
Bài tập 123 trang 95 SBT Toán 8 Tập 1
Bài tập 9.1 trang 95 SBT Toán 8 Tập 1
-


Ôn tập tứ giác
bởi Meo Lili
 14/03/2020
14/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC vuông tại A (AB
bởi Hân Nguyễn
 11/03/2020
Giúp mk vs mn ơi
11/03/2020
Giúp mk vs mn ơi Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC cân tại A, có AD là đường cao. Gọi H là trung điểm của AB, E là điểm đối xứng với D qua H. Chứng minh tứ giác AEBD là hình chữ nhật.
bởi Linh Xinh Xinh
 10/03/2020
10/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Chứng minh tứ giác AMNP là hình chữ nhật biết Cho tam giác ABC vuông tại A
bởi Chi Nguyễn
 28/02/2020
Hình chữ nhật
28/02/2020
Hình chữ nhật Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tính độ dài đường chéo hình chữ nhật
bởi Phạm Hiền
 25/12/2019
Tính do dai đuong cheo hình chu nhat
25/12/2019
Tính do dai đuong cheo hình chu nhat Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời





