Giải bài 108 tr 93 sách BT Toán lớp 8 Tập 1
Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các cạnh góc vuông bằng 5cm và 10cm (làm tròn kết quả đến chữ số thập phân thứ nhất)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng định lí Py - ta - go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
Lời giải chi tiết
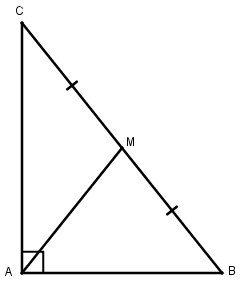
Giả sử \(∆ ABC\) có \(\widehat A = {90^0}\) , \(M\) là trung điểm của \(BC;\) \(AB = 5cm;\, AC = 10cm.\) Theo định lý Py-ta-go trong tam giác ABC vuông tại A, ta có:
\(\eqalign{ & B{C^2} = A{B^2} + A{C^2} }\)
\(\Rightarrow BC = \sqrt {{5^2} + {{10}^2}} = \sqrt {125}\) \(\approx 11,2(cm) \)
Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền nên \(AM =\eqalign {1 \over 2} BC\) (tính chất tam giác vuông)
\(⇒ AM \approx \eqalign{1 \over 2}.11,2 = 5,6\) \((cm)\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 106 trang 93 SBT Toán 8 Tập 1
Bài tập 107 trang 93 SBT Toán 8 Tập 1
Bài tập 109 trang 93 SBT Toán 8 Tập 1
Bài tập 110 trang 93 SBT Toán 8 Tập 1
Bài tập 111 trang 94 SBT Toán 8 Tập 1
Bài tập 112 trang 94 SBT Toán 8 Tập 1
Bài tập 113 trang 94 SBT Toán 8 Tập 1
Bài tập 114 trang 94 SBT Toán 8 Tập 1
Bài tập 115 trang 94 SBT Toán 8 Tập 1
Bài tập 116 trang 94 SBT Toán 8 Tập 1
Bài tập 117 trang 94 SBT Toán 8 Tập 1
Bài tập 118 trang 94 SBT Toán 8 Tập 1
Bài tập 119 trang 94 SBT Toán 8 Tập 1
Bài tập 120 trang 95 SBT Toán 8 Tập 1
Bài tập 121 trang 95 SBT Toán 8 Tập 1
Bài tập 122 trang 95 SBT Toán 8 Tập 1
Bài tập 123 trang 95 SBT Toán 8 Tập 1
Bài tập 9.1 trang 95 SBT Toán 8 Tập 1
-


Chứng minh tứ giác ABCD là hình chữ nhật
bởi Nguyễn Ngọc Sơn
 31/05/2019
31/05/2019
Tam giác MNI cân tại N, có hai trung tuyến IA, MB cắt nhau tại D. Gọi C, D theo thứ tự là trung điểm của các cạnh KI, MK.
a) Chứng minh rằng tứ giác ABCD là hình chữ nhật.
b) Biết MI = 18 cm, NK = 12 cm. Tính chu vi hình chữ nhật ABCD.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của BC và AC, D là điểm đối xứng với N qua M
a) CM: Tứ giác BDCM là hình bình hành
b) CM: AD = BN
c) Tia AN cắt CD ở E.
CM: CF = 2DE
Theo dõi (0) 1 Trả lời -


Chứng minh 2 tam giác DAN và HAN bằng nhau
bởi Quynh Nhu
 22/02/2019
22/02/2019
cho tam giác ABC vuông góc tại đỉnh A , đg cao AH . từ H kẻ HM vuông góc với AC và trên tia HM lấy điểm E sao cho MH = EM . kẻ HN vuông góc với AB và trên tia HN lấy điểm D sao cho NH = DN , chứng minh
a . 2 tam giác DAN và HAN bằng nhau b . DA = AE c . 3 điểm D,A,E thẳng hàng d . BD song song với CE e . nếu cho NH = 1,5 cm , HM = 2 cm thì DE = ? cmTheo dõi (0) 1 Trả lời -


Chứng minh NOPQ là hình bình hành
bởi Long lanh
 31/05/2019
31/05/2019
cho tứ giác ABCD. gọi N, O, P, Q tương ứng là trung điểm của AB, BC, CD, và DA
a)chứng minh rằng NOPQ là hình bình hành
b) nếu có thêm AC vuông góc BD, chứng minh NOPQ là hình chữ nhật
Viết giả thuyết , kết luận hộ mình với :(((
Theo dõi (0) 1 Trả lời -
ADMICRO


cho tam giác ABC vuông tại A diem M thuoc canh huyen BC goi DE và chân các đường vuông góc kẻ từ M đến cạnh AB,AC
a,tu giac ABME la hinh gi?vi sao?
b,goi I la trung diem cua DE chung minh rang AIM thang hang
Theo dõi (0) 1 Trả lời -


5 cho hình thoi ABCD, O là giao điểm hai đường chéo. vẽ đường thẳng qua B và song song với AC,vẽ đường thằng qua C và song song với BD,hai đường thẳng cắt qua nhau tại K
a tứ giác OBKC là hình ?vì sao?
b chứng minh AB=OK
c tìm điều kiện tứ giác ABCD để tứ giác OBKC là hình vuông
Theo dõi (0) 1 Trả lời







