Giải bài 114 tr 94 sách BT Toán lớp 8 Tập 1
Cho tam giác ABC vuông cân tại A, AC = 4cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB, AC.
a. Tứ giác ADME là hình gì ? Tính chu vi của tứ giác đó.
b. Điểm M ở vị trí nào trên cạnh BC thì đoạn thẳng DE có độ dài nhỏ nhất ?
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng các tính chất sau:
Tứ giác có ba góc vuông là hình chữ nhật
Trong tam giác cân, đường cao ứng với cạnh đáy đồng thời là trung tuyến.
Lời giải chi tiết
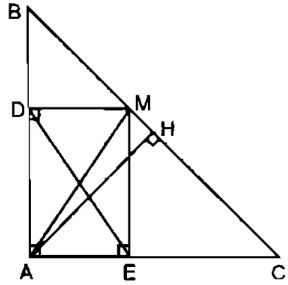
a. Xét tứ giác ADME ta có:
\(\widehat A = {90^0}\) (gt)
MD ⊥ AB (gt)
\( \Rightarrow \widehat {ADM} = {90^0}\)
ME ⊥ AC (gt)
\( \Rightarrow \widehat {AEM} = {90^0}\)
Suy ra: Tứ giác ADME là hình chữ nhật (vì có ba góc vuông)
∆ ABC vuông cân tại A \( \Rightarrow \widehat B = {45^0}\)
Suy ra: ∆ DBM vuông cân tại D ⇒ DM = DB
Chu vi hình chữ nhật ADME bằng :
2(AD + DM) = 2 ( AD + DB) = 2 AB = 2.4 = 8 (cm)
b. Gọi H là trung điểm của BC
Suy ra: AH ⊥ BC (tính chất tam giác cân)
AM ≥ AH (dấu “=” xảy ra khi M trùng với H)
Tứ giác ADME là hình chữ nhật
⇒ AM = DE (tính chất hình chữ nhật)
Suy ra: DE ≥ AH
Vậy DE = AH có độ dài nhỏ nhất khi điểm M là trung điểm của BC.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 112 trang 94 SBT Toán 8 Tập 1
Bài tập 113 trang 94 SBT Toán 8 Tập 1
Bài tập 115 trang 94 SBT Toán 8 Tập 1
Bài tập 116 trang 94 SBT Toán 8 Tập 1
Bài tập 117 trang 94 SBT Toán 8 Tập 1
Bài tập 118 trang 94 SBT Toán 8 Tập 1
Bài tập 119 trang 94 SBT Toán 8 Tập 1
Bài tập 120 trang 95 SBT Toán 8 Tập 1
Bài tập 121 trang 95 SBT Toán 8 Tập 1
Bài tập 122 trang 95 SBT Toán 8 Tập 1
Bài tập 123 trang 95 SBT Toán 8 Tập 1
Bài tập 9.1 trang 95 SBT Toán 8 Tập 1
-


Chứng minh M là trực tâm của tam giác CBN
bởi Nguyễn Thủy
 31/05/2019
31/05/2019
cho hình chữ nhật abcd ,gọi h là chân đường vuông góc hạ từ c đến bd gọi m,n,i lần lượt là trung điểm của ch ,hd,ab
a.cmr ;m là trực tâm của tam giác cbn
b.gọi k là giao điểm của bm và cn ,e là chân dường vuông góc hạ từ i đến bm .cmr eink là hcn
Theo dõi (0) 1 Trả lời -


BÀI 1:
Cho tam giác ABC vuông ở AM là đường trung tuyến . Định dạng các tam giác ABM, ACM
Bài 2
Cho tam giác ABC vuông ở A có đường trung tuyến AM. Biết AB = 6cm ; AC=8 cm. Tính độ dài các đoạn BC,AM
GIẢI DÙM MK NHA
Theo dõi (0) 1 Trả lời -


Chứng minh K là trung điểm BC biết ABCD là hình chữ nhật, I là trung điểm DH
bởi Nguyễn Hồng Tiến
 31/05/2019
31/05/2019
Cho hình chữ nhật ABCD. Kẻ AH\(\perp\)BD. Trung điểm của DH là I. Nối AI. Kẻ đường thẳng \(\perp\)với AI tại I cắt BC tại K.
Chứng minh K là trung điểm BC.
Please help meeeeeeeeeeee!!!!!




 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh trong 1 tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy và ngược lại
bởi Nguyễn Thanh Hà
 31/05/2019
31/05/2019
CMR trong 1 tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy và ngược lại
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho hình chữ nhật ABCD và 1 điểm M bất kì nằm bên trong hình chữ nhật.
Cm: \(\text{M}A^2+\text{M}C^2=\text{M}B^2+\text{M}D^2\)
Theo dõi (0) 1 Trả lời -


Cho hình chữ nhật ABCD ; Vẽ BH vuông với AC (H thuộc AC) . Gọi M là trung điểm của AH, N là trung điểm của CD.CM:BM vuông với MN
Theo dõi (0) 1 Trả lời






