Giải bài 115 tr 94 sách BT Toán lớp 8 Tập 1
Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với G qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì ? Vì sao ?
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
+) Tính chất đường trung tuyến: Cho \(∆ ABC\), có \(M\) là trung điểm \(BC\), trọng tâm \(G,\) ta có \(AG=2GM\)
Lời giải chi tiết
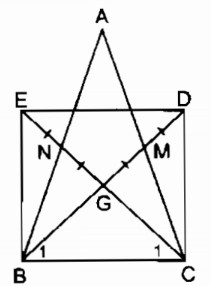
Ta có: G là trọng tâm của ∆ ABC
⇒ GB = 2GM (tính chất đường trung tuyến)
GC = 2GN (tính chất đường trung tuyến)
Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2 GM
Suy ra: GD = GD (1)
Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2 GN
Suy ra: GC = GE (2)
Từ (1) và (2) suy ra tứ giác BCDE là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Xét ∆ BCM và ∆ CBN:
BC cạnh chung
\(\widehat {BCM} = \widehat {CBN}\) (tính chất tam giác cân)
CM = BN ( vì AB = AC)
Do đó: ∆ BCM = ∆ CBN (c.g.c)
\( \Rightarrow {\widehat B_1} = {\widehat C_1}\)⇒ ∆ GBC cân tại G ⇒ GB = GC ⇒ BD = CE
Hình bình hành BCDE có hai đường chéo bằng nhau là hình chữ nhật.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 113 trang 94 SBT Toán 8 Tập 1
Bài tập 114 trang 94 SBT Toán 8 Tập 1
Bài tập 116 trang 94 SBT Toán 8 Tập 1
Bài tập 117 trang 94 SBT Toán 8 Tập 1
Bài tập 118 trang 94 SBT Toán 8 Tập 1
Bài tập 119 trang 94 SBT Toán 8 Tập 1
Bài tập 120 trang 95 SBT Toán 8 Tập 1
Bài tập 121 trang 95 SBT Toán 8 Tập 1
Bài tập 122 trang 95 SBT Toán 8 Tập 1
Bài tập 123 trang 95 SBT Toán 8 Tập 1
Bài tập 9.1 trang 95 SBT Toán 8 Tập 1
-


Chứng minh tứ giác BDEF là hình bình hành
bởi Tram Anh
 31/05/2019
31/05/2019
Cho tam giác ABC ( AB < AC ), đường cao AH, gọi D,E,F lần lượt là trung điểm các cạnh AB, AC, BC
a) Chứng minh rằng: Tứ giác BDEF là hình bình hành
b) Chứng minh rằng: Tứ giác EFHD là hình chữ nhật
c) Biết B = 60o . Hãy tính các góc của tứ giác EFHD
Theo dõi (0) 1 Trả lời -


cho \(\Delta ABC\) vuông tại A, đ/cao AH, trung tuyến AM
a) cm \(\widehat{HAB}=\widehat{MAC}\)
b) gọi D, E ll là h/chiếu của H trên AB AC. CM \(AM\perp DE\)
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác có ba góc vuông là hình chữ nhật
bởi hi hi
 31/05/2019
31/05/2019
Chứng minh rằng trong hình chữ nhật:
- Tứ giác có ba góc vuông là hcn
-Hình thang có 1 góc vuông là hcn
-hình bình hành có 1 góc vuông là hcn
hình bình hành có hai đường chéo bằng nhau là hcn
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại B.Gọi D là trung điểm của cạnh AC .Trên tia đối của tia DB lấy điểm E sao cho DB=DE
1.CM AB//CE
2.CM AC=2BD
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh ABCD là hình chữ nhật
bởi Dell dell
 31/05/2019
31/05/2019
cho tam giac ABC vuong tai A(AB>AC),O la trung diem cua BC,D la diem doi xung cua A qua O.
a)chung minh ABCD la hinh chu nhat
b)tren BD lay M,goi N la diem doi xung cua A qua N
Theo dõi (0) 1 Trả lời -


Chứng minh DD, có vuông góc với mặt phẳng ( A'B'C'D' )
bởi Bo Bo
 31/05/2019
31/05/2019
Cho hình hộp chữ nhật ABCD.A,B,C,D,
a) Đường Thẳng DD, có vuông góc với mặt phẳng ( A,B,C,D, ) không ? Vì sao ?
b) Mặt phẳng ( CDD,C, ) có vuông góc với mặt phẳng( A,B,C,D, ) không ? Vì sao ?
Theo dõi (0) 1 Trả lời





