Giải bài 110 tr 93 sách BT Toán lớp 8 Tập 1
Chứng minh rằng các tia phân giác các góc của một hình bình hành cắt nhau tao thành một hình chữ nhật.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng: Tổng ba góc trong tam giác bằng \(180^0\)
Lời giải chi tiết
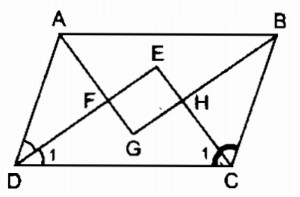
Giả sử ABCD là hình bình hành.
Gọi \(G,\, H,\, E, \,K\) lần lượt là giao điểm của các đường phân giác của \(\widehat A\) và \(\widehat B\); \(\widehat B\) và \(\widehat C\); \(\widehat C\) và \(\widehat D\); \(\widehat D\) và \(\widehat A\).
Ta có: \(\widehat {ADF} = \eqalign{1 \over 2}\widehat {ADC}\) (tính chất tia phân giác)
\(\widehat {DAF} =\eqalign {1 \over 2}\widehat {DAB}\) (tính chất tia phân giác)
\(\widehat {ADC} + \widehat {DAB} = {180^0}\) (hai góc trong cùng phía)
Suy ra: \(\widehat {ADF} + \widehat {DAF} = \eqalign{1 \over 2}\left( {\widehat {ADC} + \widehat {DAB}} \right)\) \(=\eqalign {1 \over 2}{.180^0} = {90^0}\)
Trong \(∆ AFD\) ta có:
\(\widehat {AFD} = {180^0} - \left( {\widehat {ADF} + \widehat {DAF}} \right) \) \(= {180^0} - {90^0} = {90^0}\)
\(\widehat {EFG} = \widehat {AFD}\) (đối đỉnh)
\(\eqalign{ & \Rightarrow \widehat {EFG} = {90^0} \cr & \widehat {GAB} = \eqalign{1 \over 2}\widehat {DAB}(gt) \cr & \widehat {GBA} = {1 \over 2}\widehat {CBA}(gt) \cr} \)
\(\widehat {DAB} + \widehat {CBA} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {GBA} + \widehat {GAB}\) \(= \eqalign{1 \over 2}\left( {\widehat {DAB} + \widehat {CBA}} \right)\) \(= \eqalign{1 \over 2}{.180^0} = {90^0}\)
Trong \(∆ AGB\) ta có: \(\widehat {AGB} = {180^0} - \left( {\widehat {GAB} + \widehat {GBA}} \right) \) \(= {180^0} - {90^0} = {90^0}\)
hay \(\widehat G = {90^0}\)
\(\eqalign{ & \widehat {EDC} = \eqalign{1 \over 2}\widehat {ADC}(gt) \cr & \widehat {ECD} =\eqalign {1 \over 2}\widehat {BCD}(gt) \cr} \)
\(\widehat {ADC} + \widehat {BCD} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {EDC} + \widehat {ECD} \) \(= \eqalign{1 \over 2}\left( {\widehat {ADC} + \widehat {BCD}} \right) \) \(= \eqalign{1 \over 2}{.180^0} = {90^0}\)
Trong \(∆ EDC\) ta có: \(\widehat {DEC} = {180^0} - \left( {\widehat {EDC} + \widehat {ECD}} \right)\) \(= {180^0} - {90^0} = {90^0}\) hay \(\widehat E = {90^0}\)
Vậy tứ giác EFGH là hình chữ nhật (vì có ba góc vuông).
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 108 trang 93 SBT Toán 8 Tập 1
Bài tập 109 trang 93 SBT Toán 8 Tập 1
Bài tập 111 trang 94 SBT Toán 8 Tập 1
Bài tập 112 trang 94 SBT Toán 8 Tập 1
Bài tập 113 trang 94 SBT Toán 8 Tập 1
Bài tập 114 trang 94 SBT Toán 8 Tập 1
Bài tập 115 trang 94 SBT Toán 8 Tập 1
Bài tập 116 trang 94 SBT Toán 8 Tập 1
Bài tập 117 trang 94 SBT Toán 8 Tập 1
Bài tập 118 trang 94 SBT Toán 8 Tập 1
Bài tập 119 trang 94 SBT Toán 8 Tập 1
Bài tập 120 trang 95 SBT Toán 8 Tập 1
Bài tập 121 trang 95 SBT Toán 8 Tập 1
Bài tập 122 trang 95 SBT Toán 8 Tập 1
Bài tập 123 trang 95 SBT Toán 8 Tập 1
Bài tập 9.1 trang 95 SBT Toán 8 Tập 1
-


Chứng minh EFDH là hình thang cân
bởi Trần Phương Khanh
 31/05/2019
31/05/2019
Cho tam giác giác ABC vuông tại A, đường cao AH. Gọi D,E,F lần lượt là trung điểm của các cạnh AB,BC,AC.
a. Chứng minh DF là đường trung trực của AH
b. Tính góc DHF
c. Chứng minh EFDH là hình thang cân
Giúp mk với
Chứng minh càng nhiều cách càng tốt nha
Theo dõi (0) 1 Trả lời -


Chứng minh AC,BD,EG,HF đồng quy
bởi minh thuận
 31/05/2019
31/05/2019
Cho hcn ABCD gọi E,F,G,H lần lượt là tdiem của AB,BC,CD,AD. AC cắt BD tại O, cminh: a) HEFG là hình thoi. b) AC,BD,EG,HF đồng quy
Theo dõi (0) 1 Trả lời -


cho tam giac ABC vung tại A . Gọi D là trung điểm cua BC . Từ D kẻ DM vuông góc AB ( M thuộc AB ) DN vuông góc vs AC ( N thuộc AC) .trên tia DN lấy điểm E sao cho N là trung điểm của DE
a, tứ giác AMDN là hình gì .vì sao
b, cm N là trung điểm AC
c, tứ giác ADCE là hình gì. vì sao
d , tam giác ABC cần có thêm dieu kien gi de tu giac ABCE là h. thang cân
♂✔ GIÚP VS CẢM ON TRUOC ⚡
Theo dõi (0) 1 Trả lời -


Chứng minh 3 điểm M,N,O thẳng hàng biết O là giao điểm của AH và EC, N là trung điểm của AC
bởi Trần Bảo Việt
 31/05/2019
31/05/2019
Cho tam giác ABC cân tại A, đường cao AH. Gọi M là trung điểm của AB, vẽ E đối xứng với H qua M a, Tứ giác AHBE là hình gì? Vì sao?
b, CM. AEHC là hình bình hành
c, Gọi O là giao điểm của AH và EC, N là trung điểm của AC. CM 3 điểm M,N,O thẳng hàng
Giúp mình nhanh nha....Thanks trước
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh CH//IM biết hình chữ nhật ABCD có E là chân đường vuông góc kẻ từ B đến AC
bởi Lan Anh
 31/05/2019
31/05/2019
Cho hình chữ nhật ABCD gọi E là chân đường vuông góc kẻ từ B đến AC, I là trung điểm của AE, M là trung điểm của CD a, gọi H là trung điểm của BE. Chứng minh rằng CH//IM b, Tính số đo góc BIM
Theo dõi (0) 1 Trả lời -


Chứng minh DI // EK với I là trung điểm của HB
bởi hi hi
 31/05/2019
31/05/2019
Bài 1: Cho tgABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC.
a) C/m: AH = DE
b) Gọi I là trung điểm của HB, K là trung điểm của HC. Chứng minh: DI // EK
Bài 2: Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Biết HD=2cm, BH=6cm. Tính AB, AD (làm tròn đến hàng đơn vị)
Theo dõi (0) 1 Trả lời





