Giải bài 2 tr 18 sách GK Toán Hình lớp 12
Cho hình lập phương (H). Gọi (H’) là hình bát diện đều có các đỉnh là tâm các mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H’).
Hướng dẫn giải chi tiết bài 2
Cho hình lập phương ABCD.A’B’C’D’ . Gọi E, F, G, I, J, K là tâm của các mặt của nó. Khi đó các đỉnh E, F, G, I, J, K tạo thành hình bát diện đều EFGIJK.
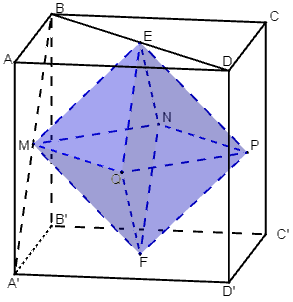
Đặt AB = a
Diện tích tam giác đều (EFJ) bằng \(\frac{{\sqrt 3 }}{8}{a^2}\).
Suy ra diện tích toàn phần của hình bát diện (H’) bằng \(\sqrt 3 {a^2}\). Diện tích toàn phần của hình lập phương (H) bằng \(6{a^2}\). Do đó tỉ số diện tích toàn phần của (H) và (H') bằng \(\frac{{6{a^2}}}{{\sqrt 3 {a^2}}} = \frac{6}{{\sqrt 3 }} = 2\sqrt 3 \).
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 1 trang 18 SGK Hình học 12
Bài tập 3 trang 18 SGK Hình học 12
Bài tập 4 trang 18 SGK Hình học 12
Bài tập 1.6 trang 12 SBT Hình học 12
Bài tập 1.7 trang 12 SBT Hình học 12
Bài tập 1.8 trang 12 SBT Hình học 12
Bài tập 1.9 trang 12 SBT Hình học 12
Bài tập 6 trang 15 SGK Hình học 12 NC
Bài tập 7 trang 15 SGK Hình học 12 NC
Bài tập 8 trang 15 SGK Hình học 12 NC
Bài tập 9 trang 15 SGK Hình học 12 NC
Bài tập 10 trang 15 SGK Hình học 12 NC
Bài tập 11 trang 20 SGK Hình học 12 NC
Bài tập 12 trang 20 SGK Hình học 12 NC
Bài tập 13 trang 20 SGK Hình học 12 NC
-
Cho một khối tứ diện đều. Hãy chứng minh rằng: Các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều.
bởi Ngoc Tiên
06/06/2021
Cho một khối tứ diện đều. Hãy chứng minh rằng: Các trọng tâm của các mặt của nó là các đỉnh của một khối tứ diện đều.
Theo dõi (0) 1 Trả lời -
Chứng minh rằng phép vị tự biến mỗi đường thẳng thành một đường thẳng song song hoặc trùng với nó, biến mỗi mặt phẳng thành một mặt phẳng song song hoặc trùng với mặt phẳng đó.
bởi Lê Văn Duyệt
07/06/2021
Chứng minh rằng phép vị tự biến mỗi đường thẳng thành một đường thẳng song song hoặc trùng với nó, biến mỗi mặt phẳng thành một mặt phẳng song song hoặc trùng với mặt phẳng đó.
Theo dõi (0) 1 Trả lời -
Có thể chia (H1) thành bao nhiêu khối lập phương bằng (H0) ?
.png)
Theo dõi (0) 1 Trả lời -
Chứng minh rằng: Các đoạn thẳng \(AF, BD\) và \(CE\) đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
bởi Ngoc Nga
05/06/2021
Cho hình bát diện đều \(ABCDEF\)
.jpg)
Chứng minh rằng: Các đoạn thẳng \(AF, BD\) và \(CE\) đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.
Theo dõi (0) 1 Trả lời -
ADMICRO
Chứng minh tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
bởi Anh Tuyet
05/06/2021
Chứng minh tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
Theo dõi (0) 1 Trả lời
