Giải bài 1.6 tr 13 SBT Toán 11
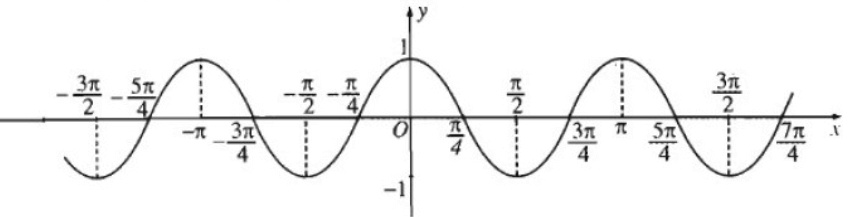
a) Chứng minh rằng cos2(x+kπ) = cos2x, k ∈ Z. Từ đó vẽ đồ thị hàm số y = cos2x
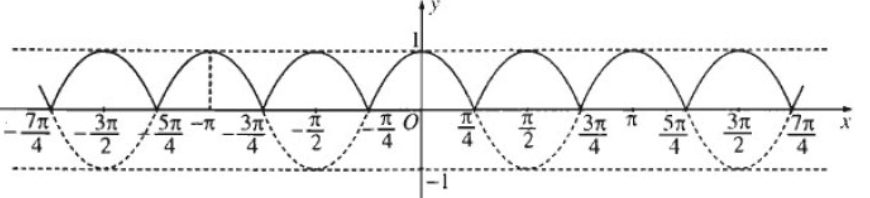
b) Từ đồ thị hàm số y = cos2x, hãy vẽ đồ thị hàm số y = |cos2x|
Hướng dẫn giải chi tiết
a) cos2(x+kπ) = cos(2x+k2π) = cos2x,k∈Z
Vậy hàm số y = cos2x là hàm số chẵn, tuần hoàn, có chu kỳ π.
Đồ thị hàm số đi qua các điểm \(\left( {0;1} \right),\left( { - \frac{\pi }{4};0} \right),\left( {\frac{\pi }{4};0} \right),\left( { - \frac{\pi }{2}; - 1} \right),\left( {\frac{\pi }{2};1} \right)\).
b) Đồ thị hàm số y = |cos2x| gồm:
+ Phần đồ thị phía trên trục Ox của đồ thị hàm số y = cos2x
+ Phần đồ thị có được từ việc lấy đối xứng phần đồ thị phía dưới trục Ox của đồ thị hàm số y = cos2x.
Đồ thị hàm số y = |cos2x| là:
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 1.4 trang 13 SBT Toán 11
Bài tập 1.5 trang 13 SBT Toán 11
Bài tập 1.7 trang 13 SBT Toán 11
Bài tập 1.8 trang 13 SBT Toán 11
Bài tập 1.9 trang 13 SBT Toán 11
Bài tập 1.10 trang 14 SBT Toán 11
Bài tập 1.11 trang 14 SBT Toán 11
Bài tập 1.12 trang 14 SBT Toán 11
Bài tập 1.13 trang 14 SBT Toán 11
Bài tập 1 trang 14 SGK Toán 11 NC
Bài tập 2 trang 14 SGK Toán 11 NC
Bài tập 3 trang 14 SGK Toán 11 NC
Bài tập 4 trang 14 SGK Toán 11 NC
Bài tập 5 trang 14 SGK Toán 11 NC
Bài tập 6 trang 15 SGK Toán 11 NC
Bài tập 7 trang 16 SGK Toán 11 NC
Bài tập 8 trang 17 SGK Toán 11 NC
Bài tập 9 trang 17 SGK Toán 11 NC
Bài tập 10 trang 17 SGK Toán 11 NC
Bài tập 11 trang 17 SGK Toán 11 NC
-


Tìm chu kì của hàm số y= sin3x + cos2x
bởi Lê Viết Khánh
 25/01/2021
25/01/2021
A. 2π
B. π
C. 4π
D. Đáp án khác
Theo dõi (0) 1 Trả lời -


Tìm chu kì của hàm số y= 2sin2x. sin4x
bởi Nguyễn Quang Minh Tú
 25/01/2021
25/01/2021
A.π/2
B. 2π
C. π
D. 4π
Theo dõi (0) 1 Trả lời -


A.π/2
B. 2π
C. 4π
D. π
Theo dõi (0) 1 Trả lời -


A. π
B. 2π
C. π/2
D. Đáp án khác
Theo dõi (0) 1 Trả lời -
ADMICRO


A. π
B. 2π
C. π/2
D. Đáp án khác
Theo dõi (0) 1 Trả lời -


Tìm chu kì của hàm số y= 2sin2x+1
bởi Mai Đào
 24/01/2021
24/01/2021
A. 1
B. 2π
C. π
D. 4π
Theo dõi (0) 1 Trả lời -


Tìm chu kì của hàm số y= ( 1)/2π cot(π/10+10 x)?
bởi Nguyễn Ngọc Sơn
 25/01/2021
25/01/2021
A. π
B. 10π
C. π/20
D. π/10
Theo dõi (0) 1 Trả lời -


Tìm chu kì của hàm số y= 10π cos(π/2-20 x)?
bởi Nguyễn Thị Thúy
 24/01/2021
24/01/2021
A. 20 π
B. 10π
C. π/20
D. π/10
Theo dõi (0) 1 Trả lời -


Hàm số y = - π.sin( 4x-2998) là
bởi nguyen bao anh
 25/01/2021
25/01/2021
A. T= π/2
B. T= π/4
C.2π
D. π
Theo dõi (0) 1 Trả lời -


Hàm số y= 2tan ( 2x-100) có chu kì là?
bởi Nguyễn Trà Long
 24/01/2021
24/01/2021
A. T= π/4
B. T= π/2
C. 2π
D. π
Theo dõi (0) 1 Trả lời -


Chu kỳ của hàm số y= tanx là:
bởi hi hi
 24/01/2021
24/01/2021
A.2π
B.π/4
C.kπ,k ∈ Z
D.π
Theo dõi (0) 1 Trả lời -


Chu kỳ của hàm số y= cosx là:
bởi Đào Lê Hương Quỳnh
 24/01/2021
24/01/2021
A. 2kπ
B. 2π/3
C. π
D. 2π
Theo dõi (0) 1 Trả lời -


A. y= sinx- x
B. y= cosx
C. y= x.sin x
D.y=(x2+1)/x
Theo dõi (0) 1 Trả lời