Bài tập 7 trang 16 SGK Toán 11 NC
Xét tính chẵn – lẻ của mỗi hàm số sau:
a. \(y = \cos \left( {x - \frac{\pi }{4}} \right)\)
b. y = tan|x|
c. y = tanx−sin2x
Hướng dẫn giải chi tiết
a) Ta có \(f\left( x \right) = \cos \left( {x - \frac{\pi }{4}} \right),\)
\(f\left( {\frac{\pi }{4}} \right) = 1,f\left( { - \frac{\pi }{4}} \right) = 0\)
Vì \(f\left( { - \frac{\pi }{4}} \right) \ne f\left( {\frac{\pi }{4}} \right)\) và \(f\left( { - \frac{\pi }{4}} \right) \ne - f\left( {\frac{\pi }{4}} \right)\)
Nên \(f\left( x \right) = \cos \left( {x - \frac{\pi }{4}} \right)\) không phải là hàm số chẵn cũng không phải là hàm số lẻ.
b) Tập xác định:
\(\forall x \in D \Rightarrow - x \in D\) và \(f\left( { - x} \right) = \tan \left| { - x} \right| = \tan \left| x \right| = f\left( x \right)\)
Do đó y = tan|x| là hàm số chẵn.
c) Tập xác định: \(D = R\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in Z} \right\}\)
\(\forall x \in D \Rightarrow - x \in D\) và f(−x) = tan(−x)–sin(−2x) = −tanx+sin2x = −(tanx–sin2x) = −f(x)
Do đó y = tanx – sin2x là hàm số lẻ.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-


Giải hpt đưa về hằng đẳng thức
bởi Ngo Thi Hien
 19/11/2019
Giải hpt đưa về hằng đẳng thức
19/11/2019
Giải hpt đưa về hằng đẳng thức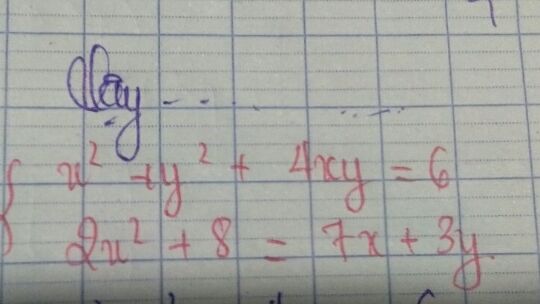 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Tập xác định
Tập xác định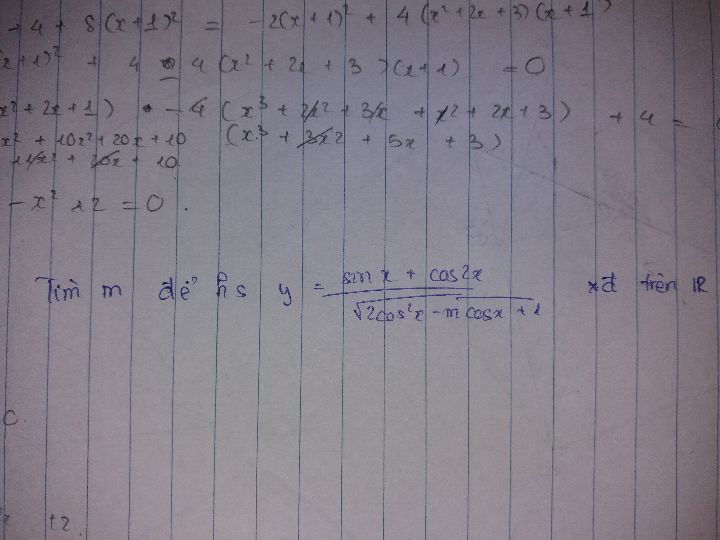 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giá trị của P=sin pi/5.cos pi/30+sin pi/30.cos 4pi/5
bởi Lê Hiền
 20/10/2019
20/10/2019
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2018;2018] để phương trình m cosx+1=0 có nghiệm?
bởi Phu Hoang Tho Nguyen
 18/10/2019
A. 1 B. 2 C.3 D. Vô sốTheo dõi (0) 2 Trả lời
18/10/2019
A. 1 B. 2 C.3 D. Vô sốTheo dõi (0) 2 Trả lời -
ADMICRO

 Tìm tập xác định
Tìm tập xác định Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


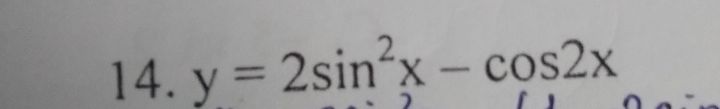 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm GTLN của hàm số y=căn(cos^2 3x+3) -2
bởi Mai Linh
 04/10/2019
04/10/2019
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chu kỳ tuần hoàn của hàm y=sin3x?
bởi Mai Linh
 04/10/2019
04/10/2019
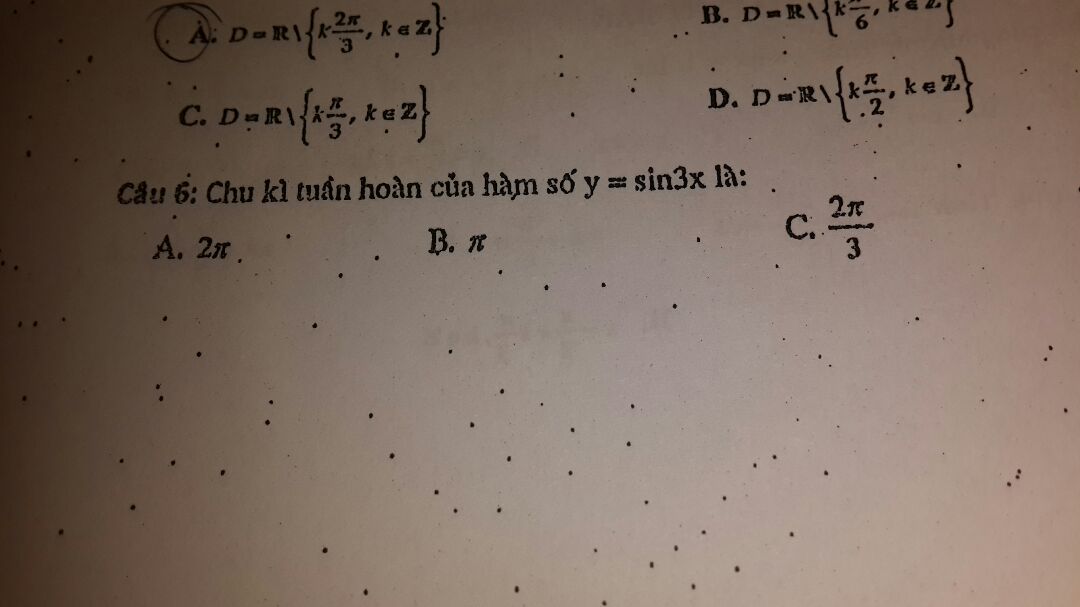 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm txđ y= tan(x-pi/4) × cot( x-pi/3)
bởi Vũ Hương Giang
 29/09/2019
Giải đáp bài tập
29/09/2019
Giải đáp bài tập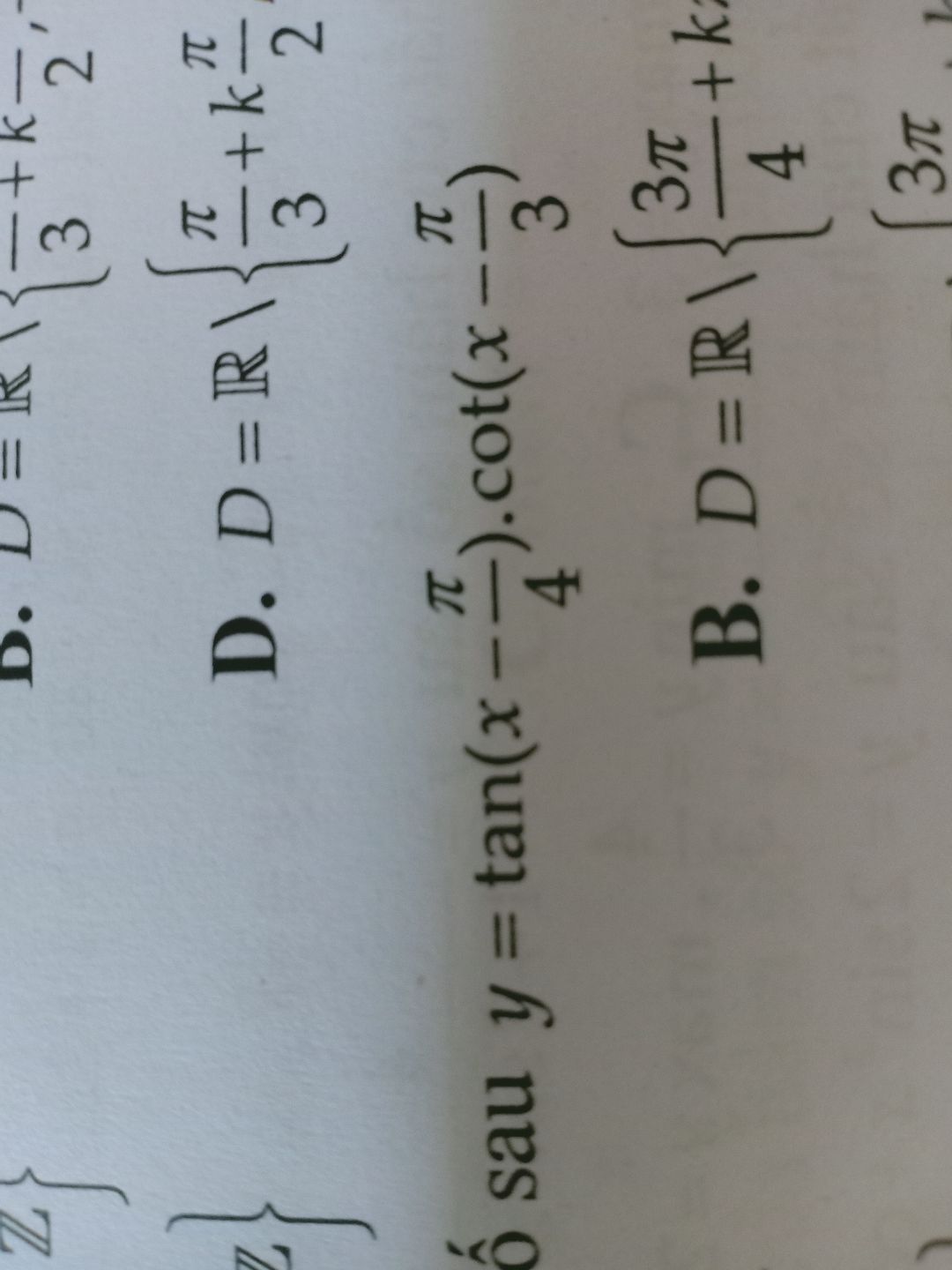 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Xét tính chẵn lẽ của hàm số y= x- 2sinx
bởi Phạm Thị Như Ý.
 25/09/2019
xét tính chẵn lẽ của hàm số y= x- 2sinxTheo dõi (0) 2 Trả lời
25/09/2019
xét tính chẵn lẽ của hàm số y= x- 2sinxTheo dõi (0) 2 Trả lời -


Tìm tập xác định của hàm số y=(sinx+1)/(sinx-2)
bởi nguyen an binh
 19/09/2019
19/09/2019
Tập xác định của hàm số y=sinx+1/sinx-2
Theo dõi (1) 6 Trả lời -


tìm gtln và gtnn của hàm số y=4cot^2 2x- căn 3(1-tan^2 x)/tan x
Theo dõi (4) 1 Trả lời



