OPTADS360
ATNETWORK
RANDOM
ON
YOMEDIA
Banner-Video
IN_IMAGE

Bài tập 13 trang 17 SGK Toán 11 NC

Lý thuyết10 Trắc nghiệm

34 BT SGK

429 FAQ

Bài tập 13 trang 17 SGK Toán 11 NC

Xét hàm số  y = f(x) = \(\cos \frac{x}{2}\)

a. Chứng minh rằng với mỗi số nguyên k, f(x+k4π) = f(x) với mọi x.

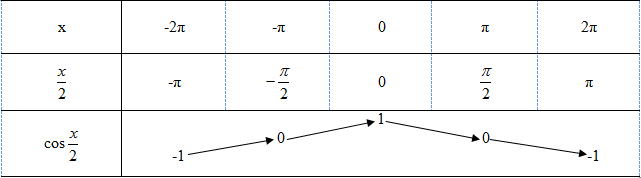
b. Lập bảng biến thiên của hàm số y = \(\cos \frac{x}{2}\) trên đoạn [−2π;2π].

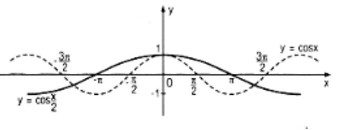
c. Vẽ đồ thị của các hàm số y = cosx và y = \(\cos \frac{x}{2}\) trong cùng một hệ trục tọa độ vuông góc Oxy.

d. Trong mặt phẳng tọa độ Oxy, xét phép biến hình F biến mỗi điểm (x;y) thành điểm (x′;y′) sao cho x′ = 2xvà y′ = y. Chứng minh rằng F biến đồ thị của hàm số y = cosx thành đồ thị của hàm số  y = \(\cos \frac{x}{2}\).

AMBIENT-ADSENSE/lession_isads=0
QUẢNG CÁO
 

Hướng dẫn giải chi tiết

a) \(f\left( {x + k4\pi } \right) = \cos \left( {\frac{\pi }{2} + k2\pi } \right) \)

\(= \cos \frac{x}{2} = f\left( x \right)\)

b) Bảng biến thiên

c) Đồ thị 

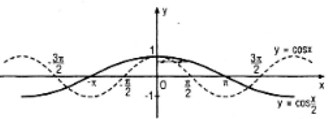
d) Nếu đặt x′ = 2x, y′ = y thì y = cosx khi và chỉ khi \(y' = \cos \frac{{x'}}{2}\). Do đó phép biến đổi xác đinh bởi (x;y)↦(x′;y′) sao cho x′ = 2x, y′ = y biến đồ thị hàm số y = cosx thành đồ thị hàm số \(y = \cos \frac{x}{2}\).

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 13 trang 17 SGK Toán 11 NC HAY thì click chia sẻ 
 
 

Bài tập SGK khác

Bài tập 11 trang 17 SGK Toán 11 NC

Bài tập 12 trang 17 SGK Toán 11 NC

NONE
OFF

XEM NHANH CHƯƠNG TRÌNH LỚP 11