Bài tập 11 trang 17 SGK Toán 11 NC

a) Đồ thị của hàm số y = −sinx là hình đối xứng qua trục hoành của đồ thị hàm số y = sinx

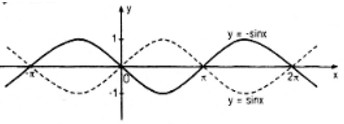
b)

Ta có \(\left| {\sin x} \right| = \left\{ \begin{array}{l}
\sin x,\,\,\,\,\sin x \ge 0\\
 - \sin x,\,\,\,\,\,\sin x < 0
\end{array} \right.\)

do đó đồ thị của hàm số y = |sinx| có được từ đồ thị (C) của hàm số y = sinx bằng cách:

- Giữ nguyên phần đồ thị của (C) nằm trong nửa mặt phẳng y ≥ 0 (tức nửa mặt phẳng bên trên trục hoành kể cả bờ Ox).

- Lấy hình đối xứng qua trục hoành của phần đồ thị (C) nằm trong nửa mặt phẳng y < 0 (tức là nửa mặt phẳng bên dưới trục hoành không kể bờ Ox);

- Xóa phần đồ thị của (C) nằm trong nửa mặt phẳng y < 0.

- Đồ thị y = |sinx| là đường liền nét trong hình dưới đây:

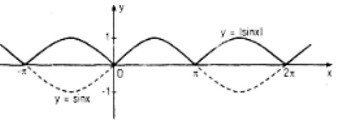
c)

Ta có:  \(\sin \left| x \right| = \left\{ \begin{array}{l}
\sin x,\,\,\,\,x \ge 0\\
 - \sin x,\,\,\,\,\,x < 0
\end{array} \right.\)

do đồ thị của hàm số y = sin|x| có được từ đồ thị (C) của hàm số y = sinx bằng cách :

- Giữ nguyên phần đồ thị của (C) nằm trong nửa mặt phẳng x ≥ 0 (tức nửa mặt phẳng bên phải trục tung kể cả bờ Oy).

- Xóa phần đồ thị của (C) nằm trong nửa mặt phẳng x < 0 (tức nửa mặt phẳng bên trái trục tung không kể bờ Oy).

- Lấy hình đối xứng qua trục tung của phần đồ thị (C) nằm trong nửa mặt phẳng x > 0

- Đồ thị y = sin|x| là đường nét liền trong hình dưới đây: 

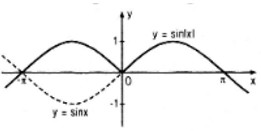
-- Mod Toán 11 HỌC247