Giải bài 2.43 tr 103 SBT Hình học 10
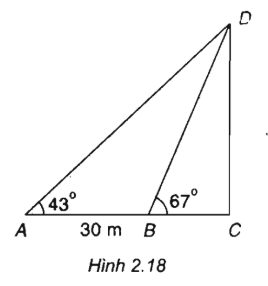
Giả sử chúng ta cần đo chiều cao CD của một cái tháp với C là chân tháp, D là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm A, B có khoảng cách AB = 30 m sao cho ba điểm A, B, C thẳng hàng người ta đo được các góc CAD = 43ο, CBD = 67ο (h.2.18). Hãy tính chiều cao CD của tháp.
Hướng dẫn giải chi tiết
Muốn tính chiều cao CD của tháp, trước hết ta hãy tính góc ADB
ADB = 67ο - 43ο = 24ο
Theo định lí sin đối với tam giác ABD ta có:
Trong tam giác vuông BCD ta có:
sin 67ο = \(\frac{{CD}}{{BD}}\)
⇒ CD = BD.sin 67ο ≈ 50,03. sin 67ο
Hay CD ≈ 46,30(m)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 2.41 trang 102 SBT Hình học 10
Bài tập 2.42 trang 102 SBT Hình học 10
Bài tập 2.44 trang 103 SBT Hình học 10
Bài tập 15 trang 64 SGK Hình học 10 NC
Bài tập 16 trang 64 SGK Hình học 10 NC
Bài tập 17 trang 65 SGK Hình học 10 NC
Bài tập 18 trang 65 SGK Hình học 10 NC
Bài tập 19 trang 65 SGK Hình học 10 NC
Bài tập 20 trang 65 SGK Hình học 10 NC
Bài tập 21 trang 65 SGK Hình học 10 NC
Bài tập 22 trang 65 SGK Hình học 10 NC
Bài tập 23 trang 65 SGK Hình học 10 NC
Bài tập 24 trang 66 SGK Hình học 10 NC
Bài tập 25 trang 66 SGK Hình học 10 NC
Bài tập 26 trang 66 SGK Hình học 10 NC
Bài tập 27 trang 66 SGK Hình học 10 NC
Bài tập 28 trang 66 SGK Hình học 10 NC
Bài tập 29 trang 66 SGK Hình học 10 NC
Bài tập 30 trang 66 SGK Hình học 10 NC
Bài tập 31 trang 66 SGK Hình học 10 NC
Bài tập 32 trang 66 SGK Hình học 10 NC
Bài tập 33 trang 66 SGK Hình học 10 NC
Bài tập 34 trang 66 SGK Hình học 10 NC
Bài tập 35 trang 66 SGK Hình học 10 NC
Bài tập 36 trang 66 SGK Hình học 10 NC
-
Tính diện tích S của tam giác ABC biết độ dài 3 trung tuyến là 15, 18, 27
bởi Nguyễn Trang
26/02/2020
Theo dõi (0) 0 Trả lời -
Tính các cạnh và các góc còn lại của tam giác ABC biết c=14, A=60, B=40
bởi Dương Thị Hoa
25/02/2020
Theo dõi (0) 1 Trả lời -
Câu 6 và 9 ạ
Theo dõi (1) 1 Trả lời -
Chứng minh c^2=(a-b)^2+4S.(1-cosC)/sinC
bởi Nguyễn Minh Tân
22/02/2020
c2=(a-b)2+4S*(1-cosC)/sinC
Theo dõi (0) 1 Trả lời
