Bài tập 37 trang 66 SGK Hình học 10 NC
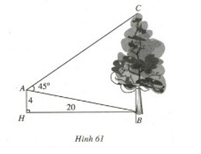
Từ vị trí A người ta quan sát một cây cao (h.61)
Biết AH = 4m, HB = 20m, BAC = 450. Tính chiều cao của cây.
Hướng dẫn giải chi tiết
Tam giác AHB vuông tại H nên AB2 = AH2+HB2 = 42+202 = 416
\(\begin{array}{*{20}{l}}
{ \Rightarrow AB \approx 20,4}\\
{\tan \widehat {BAH} = \frac{{HB}}{{HA}} = \frac{{20}}{4} = 5}\\
{ \Rightarrow \widehat {BAH} \approx 78,{7^0}}\\
{ \Rightarrow \widehat {HAC} \approx 78,{7^0} + {{45}^0} \approx 123,{7^0}}\\
{\widehat {HAB} + \widehat {HBA} = {{90}^0}}\\
{\widehat {ABC} + \widehat {HBA} = {{90}^0}}\\
{ \Rightarrow \widehat {HAB} = \widehat {ABC}}\\
\begin{array}{l}
\Rightarrow \widehat {BCA} = {180^0} - \widehat {BAC} - \widehat {ABC}\\
= {180^0} - \widehat {HAC}
\end{array}\\
{ \Rightarrow \widehat {BCA} \approx {{180}^0} - 123,{7^0} = 56,{3^0}}
\end{array}\)
Ta có:
\(\begin{array}{l}
\frac{{BC}}{{\sin {{45}^0}}} = \frac{{AB}}{{\sin 56,{3^0}}}\\
\Rightarrow BC = \frac{{20,4}}{{\sin 56,{3^0}}}.\sin {45^0} \approx 17,4
\end{array}\)
Vậy cây cao 17,4m.
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





