Giải bài 11 tr 107 sách GK Toán Đại số 10
a) Bằng cách sử dụng hằng đẳng thức a2 - b2 = (a - b)(a + b) hãy xét dấu f(x) = x4 - x2 + 6x - 9 và \(g(x) = {x^2} - 2x - \frac{4}{{{x^2} - 2x}}\)
b) Hãy tìm nghiệm nguyên của bất phương trình sau:
x(x3 - x + 6) > 9
Hướng dẫn giải chi tiết
Lưu ý: Phần bài làm hơi tắt một chút, các bạn có thể tự mình lập bảng xét dấu cho đầy đủ và rõ ràng hơn
a) Ta có: f(x) = x4 - x2 + 6x - 9
= x4 - (x - 3)2 = (x2 + x - 3)(x2 - x + 3)
Do (x2 - x + 3) = \({\left( {x - \frac{1}{2}} \right)^2} + \frac{{13}}{4}\) > 0 nên f(x) cùng dấu với (x2 + x - 3).
Tam thức x2 + x - 3 có hai nghiệm là \(\frac{{ - 1 - \sqrt {13} }}{2}\) và \(\frac{{ - 1 + \sqrt {13} }}{2}\)
Vậy f(x) < 0 khi x ∈ \(\left( {\frac{{ - 1 - \sqrt {13} }}{2};\frac{{ - 1 + \sqrt {13} }}{2}} \right)\)
f(x) > 0 khi x ∈ (-∞; \(\frac{{ - 1 - \sqrt {13} }}{2}\)) ∪ (\(\frac{{ - 1 + \sqrt {13} }}{2}\);+∞)
\(\begin{array}{l}
g(x) = {x^2} - 2x - \frac{4}{{{x^2} - 2x}}\\
= \frac{{{{\left( {{x^2} - 2x} \right)}^2} - 4}}{{{x^2} - 2x}} = \frac{{\left( {{x^2} - 2x + 2} \right)\left( {{x^2} - 2x - 2} \right)}}{{{x^2} - 2x}}
\end{array}\)
Vì x2 - 2x + 2 = (x - 1)2 + 1 > 0 nên g(x) cùng dấu với \(\frac{{\left( {{x^2} - 2x - 2} \right)}}{{{x^2} - 2x}}\)
Tam thức x2 - 2x - 2 có hai nghiệm là x1 = 1 - √3; x2 = 1 + √3.
Tam thức x2 - 2x có hai nghiệm là x1 = 0; x2 = 2
Vậy g(x) < 0 khi x ∈ (1 - √3; 0) ∪ (2; 1 + √3)
g(x) > 0 khi x ∈ (-∞; 1 - √3) ∪ (0; 2) ∪ (1 + √3; +∞)
b) Ta có: x(x3 - x + 6) > 9 ⇔ x4 - x2 + 6x - 9 > 0
⇔ x4 - (x - 3)2 > 0 ⇔ (x2 - x + 3)(x2 - x - 3) > 0 (*)
Do x2 - x + 3 = x2 - 2.x.1/2 + 1/4 + 11/4 = (x - 1/2)2 + 11/4 > 0 nên (*) tương đương với:
x2 - x - 3 > 0
⇔ x < \(\frac{{ - 1 - \sqrt {13} }}{2}\) hoặc x > \(\frac{{ - 1 + \sqrt {13} }}{2}\) (kết quả phần a)
Vậy nghiệm của bất phương trình là: \(T = \left( { - \infty ;\frac{{ - 1 - \sqrt {13} }}{2}} \right)\left( {\frac{{ - 1 + \sqrt {13} }}{2}; + \infty } \right)\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 9 trang 107 SGK Đại số 10
Bài tập 10 trang 107 SGK Đại số 10
Bài tập 12 trang 107 SGK Đại số 10
Bài tập 13 trang 107 SGK Đại số 10
Bài tập 14 trang 107 SGK Đại số 10
Bài tập 15 trang 108 SGK Đại số 10
Bài tập 16 trang 108 SGK Đại số 10
Bài tập 17 trang 108 SGK Đại số 10
Bài tập 4.76 trang 125 SBT Toán 10
Bài tập 4.77 trang 125 SBT Toán 10
Bài tập 4.78 trang 125 SBT Toán 10
Bài tập 4.79 trang 125 SBT Toán 10
Bài tập 4.80 trang 125 SBT Toán 10
Bài tập 4.81 trang 125 SBT Toán 10
Bài tập 4.82 trang 125 SBT Toán 10
Bài tập 4.83 trang 126 SBT Toán 10
Bài tập 4.84 trang 126 SBT Toán 10
Bài tập 76 trang 155 SGK Toán 10 NC
Bài tập 77 trang 155 SGK Toán 10 NC
Bài tập 78 trang 155 SGK Toán 10 NC
Bài tập 79 trang 155 SGK Toán 10 NC
Bài tập 80 trang 155 SGK Toán 10 NC
Bài tập 81 trang 155 SGK Toán 10 NC
Bài tập 82 trang 155 SGK Toán 10 NC
Bài tập 83 trang 156 SGK Toán 10 NC
Bài tập 84 trang 156 SGK Toán 10 NC
Bài tập 85 trang 156 SGK Toán 10 NC
Bài tập 86 trang 156 SGK Toán 10 NC
Bài tập 87 trang 156 SGK Toán 10 NC
-


Giải bất phương trình 2/(x-1) < = 5/(2x-1)
bởi Đinh Hạnh
 12/02/2020
giúp em với ạ
12/02/2020
giúp em với ạ Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Giải bất phương trình căn(x+3)-căn(x-1) < căn(x-2)
bởi Phương Khiêm
 10/02/2020
Căn x 3 - căn x-1 < căn x-2Theo dõi (0) 1 Trả lời
10/02/2020
Căn x 3 - căn x-1 < căn x-2Theo dõi (0) 1 Trả lời -

 Câu 2,3,4,6,7,9
Câu 2,3,4,6,7,9 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải bất phương trình căn (x^2-3x+4) < = 2x-4
bởi Châu Anh
 04/02/2020
04/02/2020
 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -
ADMICRO


Bất đẳng thức nào sau đây đúng với mọi a?
bởi TúAnhh Nguyễnn
 01/02/2020
Cho a là số thực bất kì, P=2a/a^2 1. Bất đẳng thức nào sau đây đúng với mọi a
01/02/2020
Cho a là số thực bất kì, P=2a/a^2 1. Bất đẳng thức nào sau đây đúng với mọi a Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm m để f(x)=mx^2-x-1 luôn dương
bởi Thảo
 22/01/2020
22/01/2020
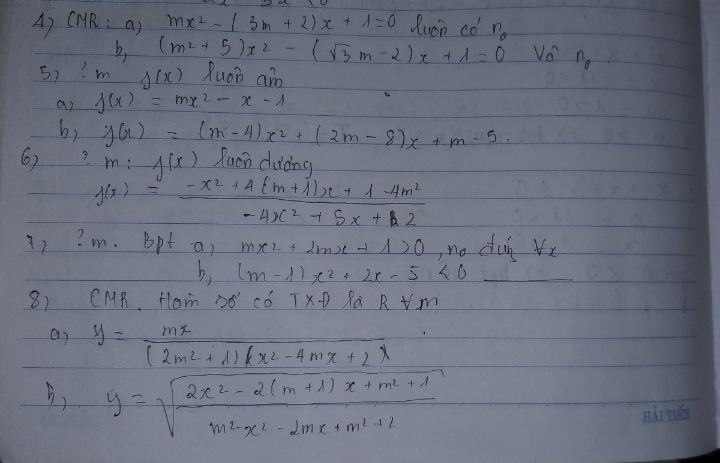 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để (m+1)x^2+4(m+1)x+m < 0 với mọi x thuộc R
bởi bảo trần
 21/01/2020
Giúp em câu 9 câu 10 trắc nghiệm và bài 3 4 tự luận với ạaaaaa
21/01/2020
Giúp em câu 9 câu 10 trắc nghiệm và bài 3 4 tự luận với ạaaaaa Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -

 Làm giúp mình bài 6,9 với
Làm giúp mình bài 6,9 với Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Cho x + y = 2019. Tìm giá trị nhỏ nhất của biểu thức
Theo dõi (0) 0 Trả lời -


Chứng minh a^3/(b+2)^2+b^3/(a+2)^2 > = 1 biết a+b=4
bởi Thùy Trang
 28/12/2019
28/12/2019
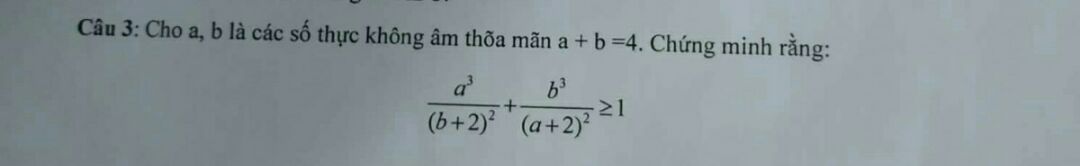 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để phương trình x^2-4x-m+5=0 có 2 nghiệm
bởi Tran Huongg Quynh
 26/12/2019
Giúp tôi
26/12/2019
Giúp tôi Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm giá trị lớn nhất của m = ab+4b biết số dương a và b thỏa mãn a+b = 10
bởi Nguyễn Thu Hương
 23/12/2019
23/12/2019
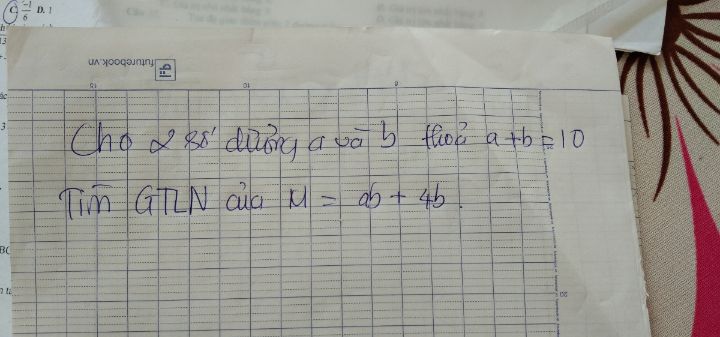 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


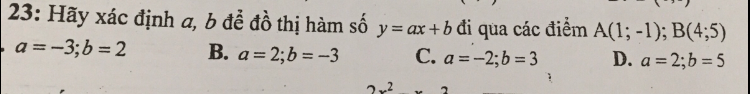 Theo dõi (3) 2 Trả lời
Theo dõi (3) 2 Trả lời -


Giải hệ phương trình 2 căn(2x+y)=3-2x-y và x^2-2xy-y^2=2
bởi phạm ánh
 12/12/2019
Câu6 ạ Giải hệ phương trình
12/12/2019
Câu6 ạ Giải hệ phương trình Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


a) Chứng minh : (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
b) Chứng minh bất dẳng thức Bunhiacôpxki : (ac + bd)2 ≤ (a2 + b2)(c2 + d2)
3. Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức : S = x2 + y2.
Theo dõi (0) 0 Trả lời -


Chứng minh 1/(x^2+y^2)+1/xy+3xy > = 27/4
bởi tran khanh quoc
 10/09/2019
10/09/2019
cho x,y>0 và x+y=1
CMR:
+
+3xy
giúp mk vs mk đang cần gấp :))
Theo dõi (0) 0 Trả lời -


Cho
thỏa mãn
. Chứng minh rằng:
Theo dõi (0) 2 Trả lời -


Tìm min 1/x^3+y^3 +1/xy biết x, y > 0 và x+y=1
bởi mạnh lê
 17/08/2019
17/08/2019
1.cho x,y>0 và x+y=căn 10.tìm min (1+x^4)(1+y^4)
2.cho
x, y>0 và x+y=1.tìm min 1/x^3+y^3 +1/xyMN ƠI GIÚP E GIẢI BÀI NI VỚI
MAI E ĐI HOK RỒI
Theo dõi (0) 0 Trả lời -


Tìm GTNN của A=2/(1-x)+1/x với 0 < x < 1
bởi Trung Bii
 12/08/2019
12/08/2019
A=2/1-x +1/x với 0<x<1
Theo dõi (0) 1 Trả lời -


Tìm GTNN của P=a/(1+b^2)+b/(1+c^2)+c/(1+a^2)
bởi Hoàn Tử
 23/07/2019
23/07/2019
Cho a, b, c là các số thực không âm biết a + b + c = 3
Tìm giá trị nhỏ nhất của P =
Theo dõi (0) 3 Trả lời -


Giải bất phương trình (2x^2-6x+7)2 < = (x^2+x+7)
bởi Hoàng Hiếu
 15/07/2019
15/07/2019
(2x2-6x+7)2 < (x2+x+7)
Theo dõi (2) 3 Trả lời -


Chứng minh 1/(x+y+1)+1/(y+z+1)+1/(x+z+1) < = 1
bởi Trần Hữu Thắng
 13/05/2019
13/05/2019
Cho x,y,z>0 và xyz=1. Chứng minh rằng:
Theo dõi (1) 1 Trả lời -


Giải bất phương trình căn(x^2+x-4) < 2x+3
bởi Yumie Chanh
 05/05/2019
05/05/2019
Giải và kết luận nghiệm cho mình với ạTheo dõi (1) 4 Trả lời





