Hình học 9 Bài 2: Tỷ số lượng giác của góc nhọn

Lý thuyết10 Trắc nghiệm46 BT SGK 220 FAQ

Bài trước chúng ta đã tìm hiểu về mối liên hệ giữa các cạnh và đường cao trong tam giác vuông. Bài hôm nay chúng ta sẽ tiếp tục xem là biết các cạnh của tam giác thì chúng ta có thể biết được các góc trong tam giác là bao nhiêu hay không qua bài học tỉ số lượng giác của góc nhọn

QUẢNG CÁO

1. Tóm tắt lý thuyết

1.1. Khái niệm tỉ số lượng giác của một góc nhọn

1.2. Tỉ số lượng giác của hai góc phụ nhau

2. Bài tập minh họa

2.1. Bài tập cơ bản

2.2. Bài tập nâng cao

3. Luyện tập Bài 2 Chương 1 Hình học 9

3.1 Trắc nghiệm Tỷ số lượng giác của góc nhọn

3.2 Bài tập SGK Tỷ số lượng giác của góc nhọn

4. Hỏi đáp Bài 2 Chương 1 Hình học 9

Tóm tắt lý thuyết

1.1. Khái niệm tỉ số lượng giác của một góc nhọn

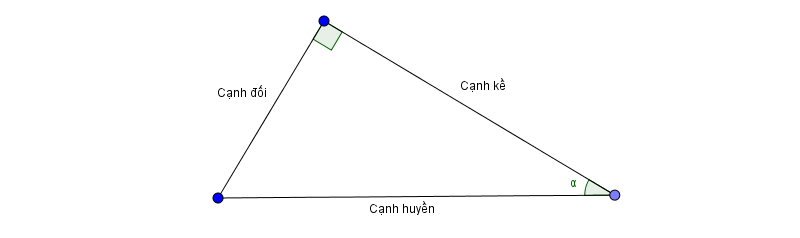
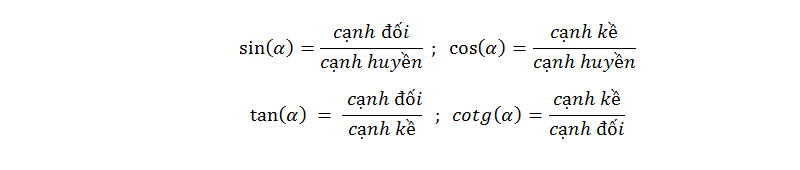Nhận xét:

Từ định nghĩa trên, dễ thấy các tỉ số lượng giác của một góc nhọn luôn luôn dương. Hơn nữa ta có: $sin\alpha < 1, cos\alpha <1$

Chú ý:

Nếu hai góc nhọn $\alpha$ và $\beta$ có $sin\alpha =sin\beta$ ( hoặc $cos\alpha =cos\beta , tan\alpha =tan\beta ,cotg \alpha =cotg\beta$ ) thì $\alpha =\beta$ vì chúng là hai góc tương ứng của hai tam giác vuông đồng dạng

1.2. Tỉ số lượng giác của hai góc phụ nhau

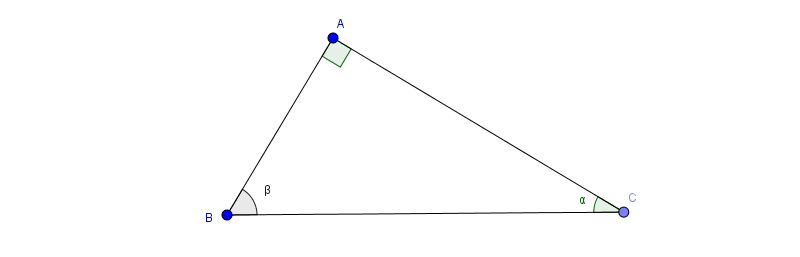Định lý:

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia

Cụ thể trong hình trên với $\alpha$ và $\beta$ là hai góc phụ nhau nên: $sin\alpha =cos\beta , cos\alpha =sin\beta, tan \alpha =cotg\beta , cotg\alpha =tan\beta$

BẢNG TỈ SỐ LƯỢNG GIÁC CÁC GÓC ĐẶC BIỆT

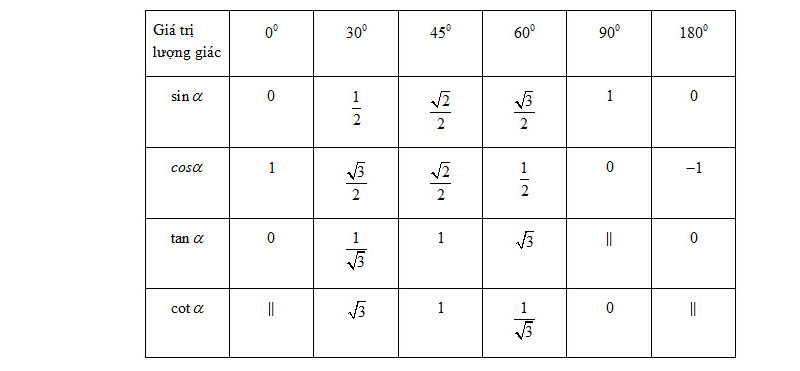Chú ý:

Từ nay khi viết các tỉ số lượng giác của một góc nhọn trong tam giác, ta bỏ kí hiệu "^". Chẳng hạn viết $sinA$ thay vì viết $sin\widehat{A}$

Từ định nghĩa các tỉ số lượng giác của một góc nhọn ta có: $tan\alpha =\frac{sin\alpha }{cos\alpha }; cotg\alpha =\frac{cos\alpha }{sin\alpha }$

và $tan\alpha .cotg\alpha =1 , sin^2\alpha +cos^2\alpha =1$; $1+tan^2\alpha =\frac{1}{cos^2\alpha }; 1+cot^2\alpha =\frac{1}{sin^2\alpha }$

(các công thức trên có thể chứng minh dễ dàng)

ADMICRO

Bài tập minh họa

2.1. Bài tập cơ bản

Bài 1: Cho tam giác ABC vuông tại A, có AB=6, BC=10. Tính sinB và cosB

Hướng dẫn: Ta có: $cosB=\frac{AB}{BC}=\frac{6}{10}=0.6 ;AC=\sqrt{BC^2-AB^2}=8 \Rightarrow sinB=\frac{AC}{BC}=0.8$

Bài 2: Chuyển các tỉ số lượng giác sau thành các tỉ số lượng giác của các góc nhỏ hơn $45^{\circ}$ : $sin72^{\circ};cos50^{\circ}; tan68^{\circ}; cotg88^{\circ}$

Hướng dẫn: Ta có: $sin72^{\circ}=cos18^{\circ};cos50^{\circ}=sin40^{\circ}; tan68^{\circ}=cotg22^{\circ}; cotg88^{\circ}=tan2^{\circ}$

Bài 3: Cho tam giác ABC. Biết cosB=0,6. Tính các tỉ số lượng giác góc C

Hướng dẫn: Ta có: $sinC=cosB=0.6$ và $cosC=sinB=\sqrt{1-cos^2B}=0.8$

$tanC=\frac{sinC}{cosC}=\frac{0.6}{0.8}=\frac{3}{4}$ và $cotC=\frac{cosC}{sinC}=\frac{0.8}{0.6}=\frac{4}{3}$

2.2. Bài tập nâng cao

Bài 1:

a) Rút gọn biểu thức: $S=cos^2\alpha +tan^2\alpha .cos^2\alpha$

b) chứng minh: $\frac{(sin\alpha +cos\alpha )^2-(sin\alpha -cos\alpha )^2}{sin\alpha .cos\alpha }=4$

Hướng dẫn:

a) $S=cos^2\alpha +tan^2\alpha .cos^2\alpha=cos^2\alpha+\frac{sin^2\alpha }{cos^2\alpha }.cos^2\alpha =sin^2\alpha +cos^2\alpha =1$

b) $VT=\frac{(1+2.sin\alpha .cos\alpha )-(1-2.sin\alpha .cos\alpha )}{sin\alpha.cos\alpha }=\frac{4.sin\alpha .cos\alpha }{sin\alpha .cos\alpha }=4$

( Áp dụng: $sin^2\alpha +cos^2\alpha =1$ )

Bài 2: Cho tam giác ABC nhọn. Gọi a, b, c lần lượt là độ dài các cạnh đối diện với các đỉnh A, B, C. Chứng minh: $\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$

Hướng dẫn:Kẻ AH vuông góc với BC ( $H\in BC$ )

Khi đó: $sinB=\frac{AH}{c}\Rightarrow sinB.c=AH$ và $sinC=\frac{AH}{b}\Rightarrow sinC.b=AH$

từ đó ta có: $sinB.c=sinC.b\Rightarrow \frac{b}{sinB}=\frac{c}{sinC}$ .

Tương tự kẻ đường cao BD ( $D\in AC$ ) sẽ chứng minh được: $\frac{a}{sinA}=\frac{b}{sinB} \Rightarrow \frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$

ADMICRO

3. Luyện tập Bài 2 Chương 1 Hình học 9

Qua bài giảng Tỷ số lượng giác của góc nhọn này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :

Khái niệm tỉ số lượng giác của một góc nhọn
Tỉ số lượng giác của hai góc phụ nhau

3.1 Trắc nghiệm Tỷ số lượng giác của góc nhọn

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Hình học 9 Bài 2 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 1:
Giá trị của biểu thức sau là bao nhiêu: $S=cos^215^{\circ}+cos^225^{\circ}+cos^235^{\circ}+cos^245^{\circ}+cos^255^{\circ}+cos^265^{\circ}+cos^275^{\circ}$
- A. $2,5$
- B. $3$
- C. $3,5$
- D. $4$
Câu 2:
Rút gọn biểu thức sau: $T=(1+cos\alpha )(1-cos\alpha )-tan^2\alpha +sin^2\alpha .tan^2\alpha$
- A. $1$
- B. $sin\alpha$
- C. $cos\alpha$
- D. $0$
Câu 3:
Cho tam giác ABC vuông tại C. Biết $cosA=\frac{5}{13}$. Khi đó tan B=??
- A. $\frac{12}{13}$
- B. $\frac{5}{12}$
- C. $\frac{12}{5}$
- D. $\frac{13}{12}$

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

3.2 Bài tập SGK Tỷ số lượng giác của góc nhọn

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Hình học 9 Bài 2 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 9 tập 1

Bài tập 10 trang 76 SGK Toán 9 Tập 1

Bài tập 11 trang 76 SGK Toán 9 Tập 1

Bài tập 12 trang 76 SGK Toán 9 Tập 1

Bài tập 13 trang 77 SGK Toán 9 Tập 1

Bài tập 14 trang 77 SGK Toán 9 Tập 1

Bài tập 15 trang 77 SGK Toán 9 Tập 1

Bài tập 16 trang 77 SGK Toán 9 Tập 1

Bài tập 17 trang 77 SGK Toán 9 Tập 1

Bài tập 22 trang 106 SBT Toán 9 Tập 1

Bài tập 24 trang 106 SBT Toán 9 Tập 1

Bài tập 25 trang 107 SBT Toán 9 Tập 1

Bài tập 26 trang 107 SBT Toán 9 Tập 1