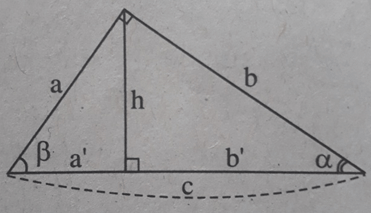
Bài tập 2.1 trang 109 SBT Toán 9 Tập 1

Tính giá trị các biểu thức sau:

1. A=\(\left(sin1^o+sin2^o+sin3^o+...+sin88^o+sin89^o\right)-\left(cos1^o+cos2^o+cos3^o+...+cos88^o+cos89^o\right)\)

2. B= \(\left(tan1^o.tan2^o.tan3^o...tan87^o.tan88^o.tan89^o\right)\)

3. C=\(cot1^o.cot2^o.cot3^o...tan87^o.tan88^o.tan89^o\)

4. D= \(sin^21^o+sin^22^o+sin^23^o+...+sin^287^o+sin^288^o+sin^289^o\)

5. E = \(cos^21^o+cos^22^o+cos^23^o+...+cos^287^o+cos^288^o+cos^289^o\)

Chứng minh hệ thức : 1+\(\cot^2_{\alpha}\)=\(\dfrac{1}{\sin^2_{\alpha}}\)

1) Chứng minh các hệ thức : a) 1+ \(\tan^2_{\alpha}\)=\(\dfrac{1}{\cos^2_{\alpha}}\)

b) \(\dfrac{\cos_{\alpha}}{1-\sin_{\alpha}}\)=1+\(\dfrac{\sin_{\alpha}}{\cos_{\alpha}}\)

2) Cho tam giác ABC vuông tại A , đường cao AH, HD , HE lần lượt là đường cao của của AHB và AHC .

Chứng minh rằng : a) \(\dfrac{AB^2}{AC^2}\) = \(\dfrac{HB}{HC}\) b) \(\dfrac{AB^3}{AC^3}\)= \(\dfrac{DB}{EC}\)

3) Cho tam giác ABC cân tại A , đường cao AH và BK . Chứng minh rằng :

\(\dfrac{1}{BK^2}\)= \(\dfrac{1}{BC^2}\)+ \(\dfrac{1}{4AH^2}\)

a) \(\sin\alpha.\cos\alpha.\left(\tan\alpha+\cot\alpha\right)\)

b)\(\cot^2-\cos^2.\cot^2\)

c)\(\tan^2-\sin^2.\tan^2\)

Đơn giản các biểu thức trên

Các cạnh của 1 tam giác tỉ lệ với 7,8,13.

a, Tính góc lớn nhất của tam giác

b, Tính diện tích biết chu vi tam giác là 84cm .

Trả lời đầy đủ nha. thank you