Bài tập 2.16 trang 110 SBT Toán 9 Tập 1
Cho tam giác ABC có \(\widehat A = {60^0}\). Chứng minh rằng: BC2 = AB2 + AC2 – AB.AC.
Hướng dẫn giải chi tiết
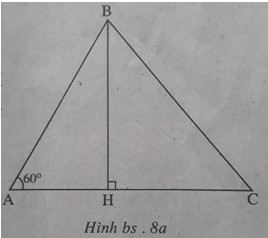
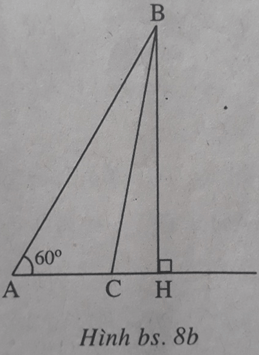
Kẻ đường cao BH của tam giác ABC thì H nằm trên tia AC (để ∠(BAC) = 60o là góc nhọn), do đó HC2 = (AC-AH)2(xem h.bs.8a, 8b)
Công thức Py-ta-go cho ta
BC2 = BH2 + HC2
= BH2 + (AC-AH)2
= BH2 + AC2 + AH2 – 2AC.AH
= AB2 + AC2 – 2AC.AH.
Do ∠(BAC) = 60o nên AH = AB.cos60o = AB/2, suy ra BC2 = AB2 + AC2 – AB.AC
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-
Tính cos^212+cos^278+cos^21+cos^289
bởi Nguyễn Xuân Ngạn
13/02/2019
Tính:
a) \(\cos^212+\cos^278+\cos^21+\cos^289\)
b) \(\sin^23+\sin^215+\sin^275+\sin^287\)
c) \(\sin^21+\sin^22+\sin^33+...+\sin^288+\sin^289\)
Theo dõi (0) 1 Trả lời -
Rút gọn biểu thức A=sin^2 10+sin^2 20+sin^2 30+sin^2 80+sin^2 70+sin^2 60
bởi Nguyễn Tiểu Ly
13/02/2019
Rút gọn biểu thức:
\(A=\sin^210+\sin^220+\sin^230+\sin^280+\sin^270+\sin^260\)
\(B=\left(1+\tan^2\alpha\right)\left(1-\sin^2\alpha\right)+\left(1+\cot^2\alpha\right)\left(1-\cos^2\alpha\right)\)
Theo dõi (0) 1 Trả lời -
cho tam giác abc có góc a = 60 độ, góc c=50 độ ac=35 cm. kẻ đường cao ah tính ha,hb,hc ( làm tròn đến chữ số thập quân thứ ba )
Theo dõi (0) 1 Trả lời -
Xếp theo thứ tự từ nhỏ đến lớn: \(\sin78^o;\cos14^o;\sin47^o;\cos87^o\)
Theo dõi (0) 1 Trả lời -
ADMICRO
Chứng minh a^2/b − 1 + b^2/a − 1 ≥ 0
bởi Bảo Lộc
21/02/2019
Cho a>1 ,b>1.CM \(\dfrac{a^2}{b-1}+\dfrac{b^2}{a-1}\ge0\) (Áp dụng bất đẳng thức Cô-si)
Theo dõi (0) 1 Trả lời
