Giải bài 3.6 tr 164 SBT Toán 12
Tính các nguyên hàm sau:
a) \(\mathop \smallint \nolimits x{\left( {3 - x} \right)^5}dx\)
b) \(\mathop \smallint \nolimits {\left( {{2^x} - {3^x}} \right)^2}dx\)
c) \(\mathop \smallint \nolimits x\sqrt {2 - 5x} dx\)
d) \(\mathop \smallint \nolimits \frac{{\ln \left( {\cos x} \right)}}{{{{\cos }^2}x}}dx\)
e) \(\mathop \smallint \nolimits \frac{x}{{{{\sin }^2}x}}dx\)
g) \(\mathop \smallint \nolimits \frac{{x + 1}}{{\left( {x - 2} \right)\left( {x + 3} \right)}}dx\)
h) \(\mathop \smallint \nolimits \frac{1}{{1 - \sqrt x }}dx\)
i) \(\int {\sin 3x\cos 2x} dx\)
Hướng dẫn giải chi tiết
a) \({I_1} = \mathop \smallint \nolimits x{\left( {3 - x} \right)^5}dx\)
Đặt \(3 - x = u \Rightarrow dx = - du\), ta có:
\(\begin{array}{l}
{I_1} = \mathop \smallint \nolimits \left( {u - 3} \right){u^5}du = \mathop \smallint \nolimits \left( {{u^6} - 3{u^5}} \right)du = \frac{1}{7}{u^7} - \frac{1}{2}{u^6} + C\\
= \frac{1}{7}{\left( {3 - x} \right)^7} - \frac{1}{2}{\left( {3 - x} \right)^6} + C
\end{array}\)
b) Ta có:
\(\begin{array}{l}
\smallint \left( {{2^x} - {3^x}} \right)2dx = \smallint \left( {{2^{2x}} - {{2.2}^x}{3^x} + {3^{2x}}} \right)dx\\
= \smallint {4^x}dx - 2\smallint {6^x}dx + \smallint {9^x}dx\\
= \frac{{{4^x}}}{{\ln 4}} - 2\frac{{{6^x}}}{{\ln 6}} + \frac{{{9^x}}}{{\ln 9}} + C
\end{array}\)
c) \({I_2} = \mathop \smallint \nolimits x\sqrt {2 - 5x} dx\)
Đặt \(\sqrt {2 - 5x} = u \Rightarrow 2 - 5x = {u^2} \Rightarrow dx = - \frac{2}{5}udu\)
Ta có: \(x = \frac{{2 - u}}{5}\) nên
\(\begin{array}{l}
{I_2} = - \mathop \smallint \nolimits \frac{{2 - u}}{5}.u.\frac{2}{5}udu = \mathop \smallint \nolimits \left( { - \frac{4}{{25}}{u^2} + \frac{2}{{25}}{u^3}} \right)du\\
= - \frac{4}{{75}}{u^3} + \frac{1}{{50}}{u^4} + C\\
= - \frac{4}{{75}}{\left( {2 - 5x} \right)^{\frac{3}{2}}} + \frac{1}{{50}}{\left( {2 - 5x} \right)^2} + C
\end{array}\)
d) \({I_3} = \mathop \smallint \nolimits \frac{{\ln \left( {\cos x} \right)}}{{{{\cos }^2}x}}dx\)
Đặt \(\left\{ \begin{array}{l}
u = \ln \left( {\cos x} \right)\\
dv = 1\cos 2xdx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = - \sin x\cos xdx\\
v = \tan x
\end{array} \right.\)
Ta có:
\(\begin{array}{l}
{I_3} = \tan x\ln \left( {\cos x} \right) + \smallint \tan x.\frac{{\sin x}}{{\cos x}}dx\\
= \tan x\ln \left( {\cos x} \right) + \smallint \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}dx\\
= \tan x\ln \left( {\cos x} \right) + \smallint \frac{{1 - {{\cos }^2}x}}{{{{\cos }^2}x}}dx\\
= \tan x\ln \left( {\cos x} \right) + \smallint \left( {\frac{1}{{{{\cos }^2}x}} - 1} \right)dx\\
= \tan x\ln \left( {\cos x} \right) + \tan x - x + C
\end{array}\)
e) \({I_4} = \mathop \smallint \nolimits \frac{x}{{{{\sin }^2}x}}dx\)
Đặt \(\left\{ \begin{array}{l}
u = x\\
dv = \frac{1}{{{{\sin }^2}x}}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = dx\\
v = - \cot x
\end{array} \right.\)
Ta có:
\({I_4} = - x\cot x + {\rm{ }}\int {\cot xdx} = - x\cot x + {\rm{ }}\int {\frac{{\cos x}}{{\sin x}}} dx\)
Đặt \(t = \sin x \Rightarrow dt = \cos xdx\). Suy ra:
\({I_4} = - x\cot x + \mathop \smallint \nolimits \frac{{dt}}{t} = - x\cot x + \ln \left| t \right| + C = - x\cot x + \ln \left| {{\rm{sinx}}} \right| + C\)
g) \({I_5} = \mathop \smallint \nolimits \frac{{x + 1}}{{\left( {x - 2} \right)\left( {x + 3} \right)}}dx\)
Ta có: \(\frac{{x + 1}}{{\left( {x - 2} \right)\left( {x + 3} \right)}} = \frac{3}{{5(x - 2)}} + \frac{2}{{5(x + 3)}}\)
Khi đó:
\({{I_5} = \mathop \smallint \nolimits \frac{3}{{5\left( {x - 2} \right)}}dx + \mathop \smallint \nolimits \frac{2}{{5\left( {x + 3} \right)}}dx = \frac{3}{5}\ln \left| {x - 2} \right| + \frac{2}{5}\ln \left| {x + 3} \right| + C}\)
h) \({I_6} = \mathop \smallint \nolimits \frac{1}{{1 - \sqrt x }}dx\)
Đặt \(u = \sqrt x \Rightarrow {u^2} = x \Rightarrow dx = 2udu\)
Ta có:
\(\begin{array}{l}
{I_6} = \mathop \smallint \nolimits \frac{{2udu}}{{1 - u}} = \mathop \smallint \nolimits \left( { - 2 + \frac{2}{{1 - u}}} \right)du\\
= - 2u + 2\ln \left| {1 - u} \right| + C\\
= - 2\sqrt x + 2ln\left| {1 - \sqrt x } \right| + C
\end{array}\)
i) \(\int {\sin 3x} \cos 2xdx = \frac{1}{2}{\rm{ }}\int {(\sin x + \sin 5x)} dx = - \frac{1}{2}\left( {\cos x + \frac{1}{5}\cos 5x} \right) + C\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.4 trang 164 SBT Toán 12
Bài tập 3.5 trang 164 SBT Toán 12
Bài tập 3.7 trang 164 SBT Toán 12
Bài tập 3.8 trang 165 SBT Toán 12
Bài tập 3.9 trang 165 SBT Toán 12
Bài tập 3.10 trang 165 SBT Toán 12
Bài tập 3.11 trang 165 SBT Toán 12
Bài tập 3.12 trang 165 SBT Toán 12
Bài tập 3.13 trang 165 SBT Toán 12
Bài tập 3.14 trang 166 SBT Toán 12
Bài tập 3.15 trang 166 SBT Toán 12
Bài tập 1 trang 141 SGK Toán 12 NC
Bài tập 2 trang 141 SGK Toán 12 NC
Bài tập 3 trang 141 SGK Toán 12 NC
Bài tập 4 trang 141 SGK Toán 12 NC
Bài tập 5 trang 145 SGK Toán 12 NC
Bài tập 6 trang 145 SGK Toán 12 NC
Bài tập 7 trang 145 SGK Toán 12 NC
-


Tìm nguyên hàm: 1/(x 1)(x 2)
bởi Ngọc Nguyễn Thị Bích
 16/01/2021
Tìm nguyên hàm của 1/(x 1)(x 2)Theo dõi (0) 0 Trả lời
16/01/2021
Tìm nguyên hàm của 1/(x 1)(x 2)Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm √x² 1 dx
bởi Kieu Hieu
 14/01/2021
Nguyên hàm √x² 1 dxTheo dõi (0) 0 Trả lời
14/01/2021
Nguyên hàm √x² 1 dxTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm của x(x2+7)15 .
bởi Bùi Tuấn
 14/01/2021
14/01/2021
Tìm nguyên hàm của x(x2+7)15 . Em có kết quả rồi nhưng vẫn chưa hiểu tại sao đặt t=x2 + 7 mà dt = 2xdx ạ ? em đáng lẽ ra phải bằng 3x2dx chứ ạ ?
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm của hàm số (sin4x) /(1 cos²x)
bởi Thư Hoài
 13/01/2021
(sin4x) /(1 cos²x)Theo dõi (0) 0 Trả lời
13/01/2021
(sin4x) /(1 cos²x)Theo dõi (0) 0 Trả lời -
ADMICRO


Tìm nguyên hàm
bởi Minh Trần
 08/01/2021
08/01/2021
 tính nguyên hàm , giúp mình 3 bài này với Theo dõi (0) 0 Trả lời
tính nguyên hàm , giúp mình 3 bài này với Theo dõi (0) 0 Trả lời -


Giá trị của f(1) bằng bao nhiêu?
bởi vanh
 28/07/2020
28/07/2020
Câu 24
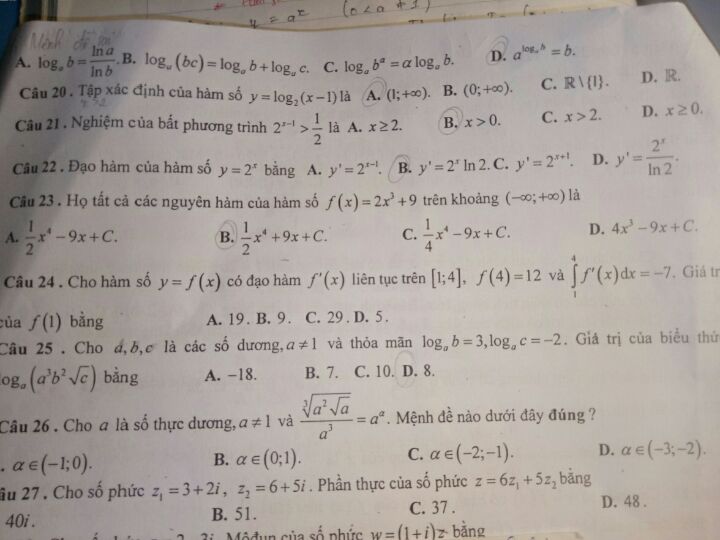 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Đạo hàm của -36ln(x 5)?
bởi Lê Thanh Thiên
 27/07/2020
27/07/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm nguyên hàm của \(e^{x^2}\)?
bởi Kiều My
 22/07/2020
22/07/2020
Nguyên hàm x nhân e mũ x bình
Theo dõi (0) 0 Trả lời -


Tính nguyên hàm \(\int {\frac{{\left( {x - 1} \right){e^x}}}{{{x^2}}}dx} \)?
bởi Nguyễn Đức
 20/07/2020
20/07/2020
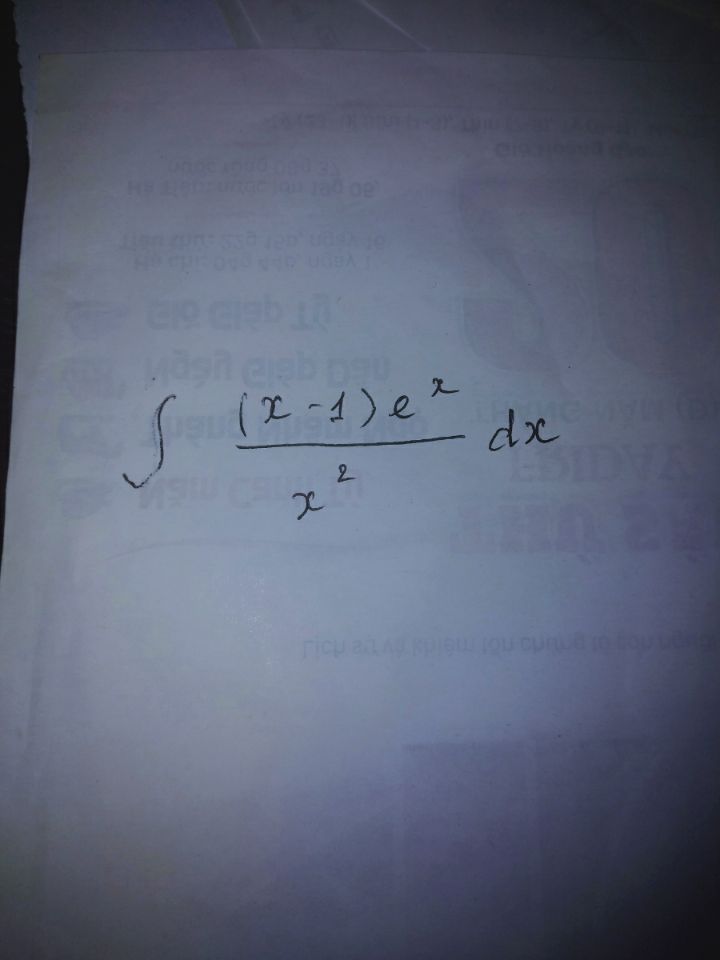 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


S= a+2b+4c là giá trị nào sau đây?
bởi Nguyễn Thị Minh Tâm
 17/07/2020
17/07/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Nguyên hàm của e mũ x bình?
bởi Nguỵ Thiên Ngân
 05/07/2020
Nguyên hàm của e mũ x bìnhTheo dõi (0) 1 Trả lời
05/07/2020
Nguyên hàm của e mũ x bìnhTheo dõi (0) 1 Trả lời -


Tính \(I = \int\limits_0^2 {f(x)dx} \)?
bởi Nguyễn Minh Hiền
 30/06/2020
30/06/2020
Câu 12b
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm \(\int {{{\sin }^4}xdx?} \)?
bởi Nguyễn Đạt
 23/06/2020
Theo dõi (0) 0 Trả lời
23/06/2020
Theo dõi (0) 0 Trả lời -


Tính \(\int {{4^{3x}}dx} \)?
bởi Nguyễn Khang BT
 21/06/2020
21/06/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính \(\int {\frac{{{e^{\ln x}}}}{x}dx} \)?
bởi y nguyen
 21/06/2020
21/06/2020
nguyên hàm của e mũ lnx chia x dx
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm I = nguyên hàm e mũ ln x chia x
Theo dõi (0) 0 Trả lời -


Nguyên hàm của hàm số f(x)=|x|?
bởi Kim Thoa
 10/06/2020
10/06/2020
Nguyên hàm của hàm số f(x)=|x|?
Theo dõi (0) 2 Trả lời -


Một vật chuyển động chậm dần với vận tốc VT = 160 - 10t mét trên giây Hỏi rằng trong 3 giây trước khi dừng hẳn vật di chuyển được bao nhiêu mét?
Theo dõi (0) 2 Trả lời -


Họ tất cả các nguyên hàm của hàm số \(f(x) = \frac{{2x + 3}}{{x - 4}}\) trên khoảng \(\left( {4; + \infty } \right)\)?
bởi Thu
 09/06/2020
09/06/2020
Giả hộ mình với ạ
Họ tất cả các nguyên hàm của hàm số \(f(x) = \frac{{2x + 3}}{{x - 4}}\) trên khoảng \(\left( {4; + \infty } \right)\)?
Theo dõi (0) 2 Trả lời -


Tính thể tích của khối tròn xoay được giới hạn bởi đường y=sinx,trục hoành và 2 đường thẳng x=0,x=π ?
bởi Trần Đình Trường
 07/06/2020
07/06/2020
Thể tích của khối tròn xoay được giới hạn bởi đường y= sinx, trục hoành và 2 đường thẳng x=0, x=π là?
Theo dõi (0) 1 Trả lời -


F(x)=2x 3/2x-1 là nguyê hàm của hàm nào
Theo dõi (0) 1 Trả lời -


Câu 6 Hàm số F(x) là một nguyên hàm của hàm số f(x) trên khoảng k nếu
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Nêu một số phương pháp tính nguyên hàm
bởi Trịnh Lan Trinh
 30/05/2020
Theo dõi (0) 1 Trả lời
30/05/2020
Theo dõi (0) 1 Trả lời




