Giải bài 3.9 tr 165 SBT Toán 12
Tính các nguyên hàm sau đây:
a) \(\mathop \smallint \nolimits (x + \ln x){x^2}dx\)
b) \(\int {(x + {{\sin }^2}x)\sin xdx} \)
c) \(\mathop \smallint \nolimits (x + {e^x}){e^{2x}}dx\)
d) \(\int {(x + \sin x)\frac{{dx}}{{{{\cos }^2}x}}} \)
Hướng dẫn giải chi tiết
a) Đặt \(\left\{ \begin{array}{l}
u = x + \ln x\\
dv = {x^2}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = \left( {1 + \frac{1}{x}} \right)dv\\
v = \frac{1}{3}{x^3}
\end{array} \right.\)
Ta có:
\(\begin{array}{l}
I = \frac{1}{3}{x^3}\left( {x + \ln x} \right) - \frac{1}{3}\smallint {x^3}\left( {1 + \frac{1}{x}} \right)dx\\
= \frac{1}{3}{x^4} + \frac{1}{3}{x^3}\ln x - \frac{1}{3}\smallint \left( {{x^3} + {x^2}} \right)dx\\
= \frac{1}{3}{x^4} + \frac{1}{3}{x^3}\ln x - \frac{1}{3}\left( {\frac{1}{4}{x^4} + \frac{1}{3}{x^3}} \right) + C4\\
= \frac{1}{4}{x^4} - \frac{1}{9}{x^3} + \frac{1}{3}{x^3}\ln x + C
\end{array}\)
b) \(J = \int {(x + {{\sin }^2}x)\sin xdx} \)
Đặt \(\left\{ \begin{array}{l}
u = x + \sin 2x\\
dv = \sin xdx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = 1 + 2\sin x\cos x\\
v = - \cos x
\end{array} \right.\)
Ta có:
\(\begin{array}{l}
J = - \cos x\left( {x + {{\sin }^2}x} \right) + \smallint \cos x\left( {1 + 2\sin x\cos x} \right)dx\\
= - x\cos x - \cos x{\sin ^2}x + \smallint \cos xdx + 2\smallint {\cos ^2}x\sin xdx\\
= - x\cos x - \cos x{\sin ^2}x + \sin x - 2\smallint {\cos ^2}xd\left( {\cos x} \right)\\
= - x\cos x - \cos x{\sin ^2}x + \sin x - \frac{2}{3}{\cos ^3}x + C
\end{array}\)
c) \(K = \mathop \smallint \nolimits (x + {e^x}){e^{2x}}dx\)
Đặt \(\left\{ \begin{array}{l}
u = x + ex\\
dv = {e^{2x}}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = \left( {1 + {e^x}} \right)dv\\
v = \frac{1}{2}{e^{2x}}
\end{array} \right.\)
Ta có:
\(\begin{array}{l}
K = \frac{1}{2}\left( {x + {e^x}} \right){e^{2x}} - \frac{1}{2}\smallint {e^{2x}}\left( {1 + {e^x}} \right)dx\\
= \frac{1}{2}\left( {x + {e^x}} \right){e^{2x}} - \frac{1}{2}\smallint \left( {{e^{2x}} + {e^{3x}}} \right)dx\\
= \frac{1}{2}x{e^{2x}} + \frac{1}{2}{e^{3x}} - \frac{1}{4}{e^{2x}} - \frac{1}{6}{e^{3x}} + C\\
= \frac{1}{2}x{e^{2x}} + \frac{1}{3}{e^{3x}} - \frac{1}{4}{e^{2x}} + C
\end{array}\)
d) \(F = \int {(x + \sin x)\frac{{dx}}{{{{\cos }^2}x}}} \)
Đặt \(\left\{ \begin{array}{l}
u = x + \sin x\\
dv = \frac{{dx}}{{{{\cos }^2}x}}
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = \left( {1 + \cos x} \right)dv\\
v = \tan x
\end{array} \right.\)
Ta có:
\(\begin{array}{l}
F = \left( {x + \sin x} \right)\tan x - \int {\left( {1 + \cos x} \right)\tan xdx} \\
= \left( {x + \sin x} \right)\tan x - \int {\left( {\frac{{\sin x}}{{\cos x}} + \sin x} \right)dx} \\
= \left( {x + \sin x} \right)\tan x + \ln \left| {\cos x} \right| + \cos x + C
\end{array}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.7 trang 164 SBT Toán 12
Bài tập 3.8 trang 165 SBT Toán 12
Bài tập 3.10 trang 165 SBT Toán 12
Bài tập 3.11 trang 165 SBT Toán 12
Bài tập 3.12 trang 165 SBT Toán 12
Bài tập 3.13 trang 165 SBT Toán 12
Bài tập 3.14 trang 166 SBT Toán 12
Bài tập 3.15 trang 166 SBT Toán 12
Bài tập 1 trang 141 SGK Toán 12 NC
Bài tập 2 trang 141 SGK Toán 12 NC
Bài tập 3 trang 141 SGK Toán 12 NC
Bài tập 4 trang 141 SGK Toán 12 NC
Bài tập 5 trang 145 SGK Toán 12 NC
Bài tập 6 trang 145 SGK Toán 12 NC
Bài tập 7 trang 145 SGK Toán 12 NC
-


Tìm nguyen hàm của (2x-1)*căn (x^2 1)
bởi Khanh Khang
 12/03/2020
Tìm nguyen hàm của (2x-1) × căn (x^2 1)dxTheo dõi (0) 2 Trả lời
12/03/2020
Tìm nguyen hàm của (2x-1) × căn (x^2 1)dxTheo dõi (0) 2 Trả lời -


Tính tích phân từ 0->1 của e^x+x^2
bởi Đoàn Minh Thư
 11/03/2020
Câu 18 ạ. Tìm họ nguyên hàm
11/03/2020
Câu 18 ạ. Tìm họ nguyên hàm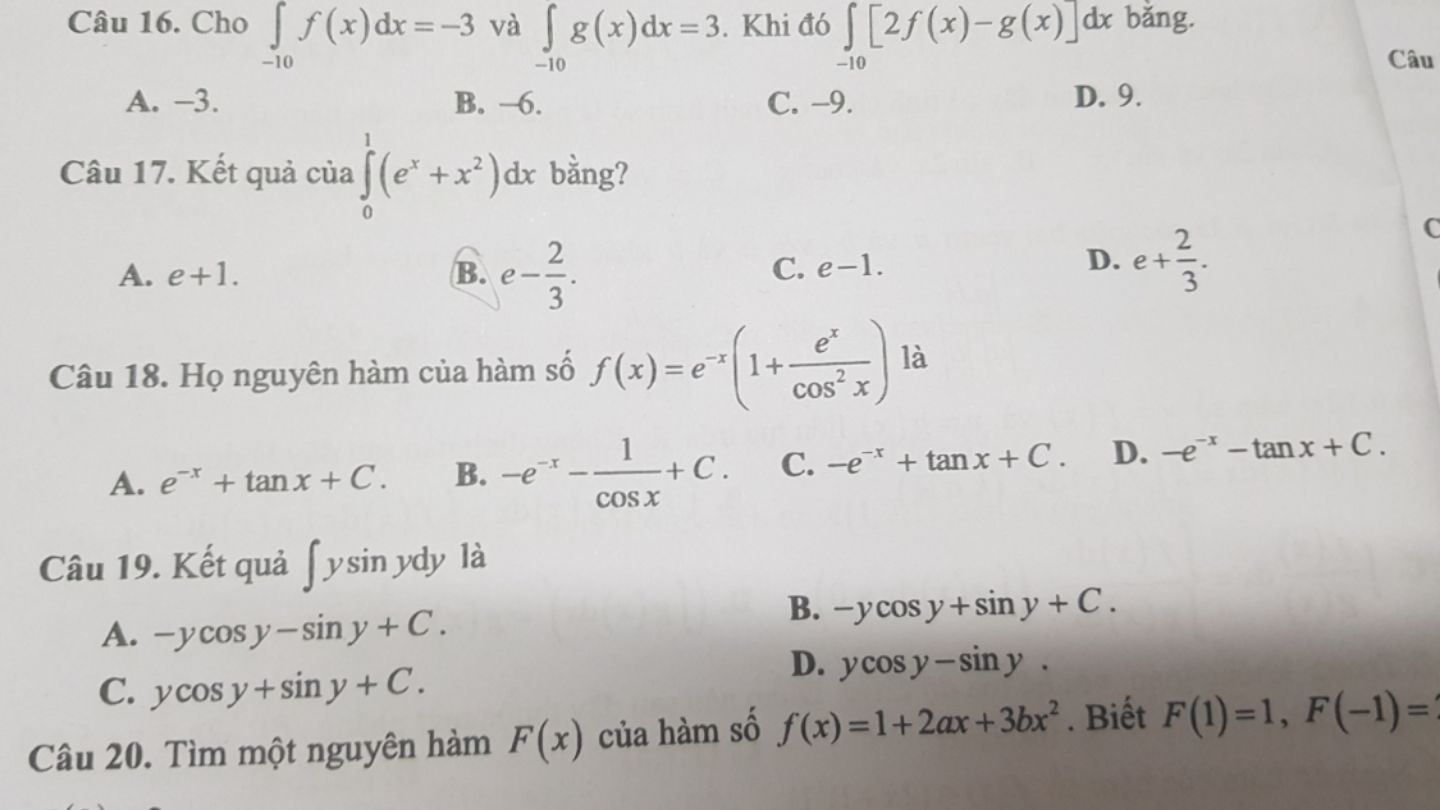 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Nguyên hàm của hàm số cos5x.cosx
bởi Quyên HT
 10/03/2020
Nguyên hàm của ham số cos5x.cosxTheo dõi (0) 4 Trả lời
10/03/2020
Nguyên hàm của ham số cos5x.cosxTheo dõi (0) 4 Trả lời -


Nguyên hàm của hàm e^[2*(3x 1)]
bởi CH Nguyễn
 10/03/2020
e^[2*(3x 1)]Theo dõi (0) 0 Trả lời
10/03/2020
e^[2*(3x 1)]Theo dõi (0) 0 Trả lời -
ADMICRO


Tìm nguyên hàm của 10 mũ 2x
bởi Trần Ngọc Mai
 09/03/2020
Tìm nguyên hàm của 10 mũ 2xTheo dõi (0) 2 Trả lời
09/03/2020
Tìm nguyên hàm của 10 mũ 2xTheo dõi (0) 2 Trả lời -


Tìm nguyên hàm y= 2x 3/2x^2-x-1
bởi Lê Linh Lan
 09/03/2020
Tìm nguyên hàmTheo dõi (0) 2 Trả lời
09/03/2020
Tìm nguyên hàmTheo dõi (0) 2 Trả lời -


Tìm nguyên hàm của hàm f(x)=x^3-3/x^2+2
bởi Đặng Thị Như Quỳnh
 08/03/2020
Nguyên hàm (2x-1)e^1/x
08/03/2020
Nguyên hàm (2x-1)e^1/x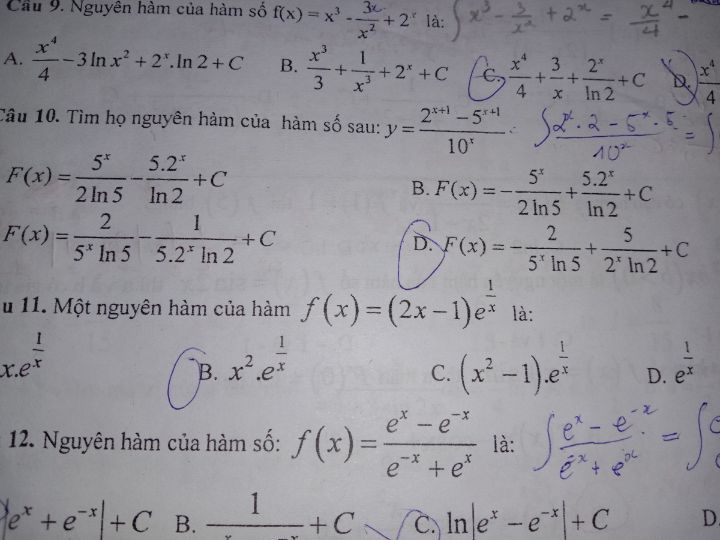 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


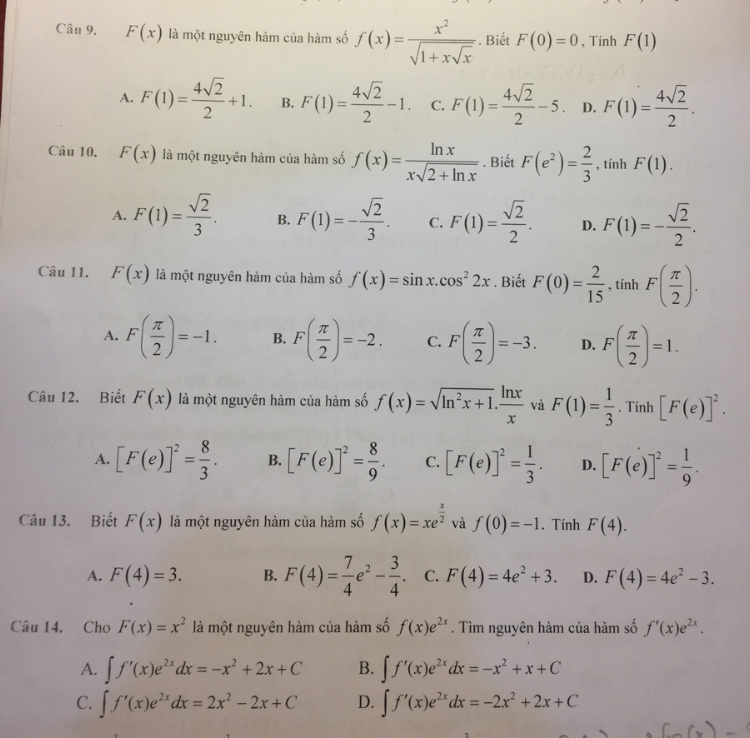 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Họ nguyên hàm của hàm số y=(2x+1)^2019
bởi Trần Đình Tuấn An
 05/03/2020
Câu 13 ạ
05/03/2020
Câu 13 ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính nguyên hàm 1/(x-2)(x-1)
bởi Nhật Hào
 05/03/2020
05/03/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tìm nguyên hàm của 2sin^2.x/2
bởi Vy Duong Thuy
 03/03/2020
Nguyên hàm của 2sin^2.x/2.dx.Giúp mình với! Cảm ơnTheo dõi (0) 2 Trả lời
03/03/2020
Nguyên hàm của 2sin^2.x/2.dx.Giúp mình với! Cảm ơnTheo dõi (0) 2 Trả lời -


Nguyên hàm của (3x-1)/(x^2+ 6x+ 9)
bởi Bích Loan
 03/03/2020
03/03/2020
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tìm nguyên hàm (2x-3)/(x^2-3x+5)
bởi Ông Lão
 02/03/2020
02/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm của (5x-3)/(x^2-3x-2)
bởi Quốc Khánh
 02/03/2020
câu d
02/03/2020
câu d Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Nguyên hàm của f(x)=cos3x.cosx?
bởi Thuc Vy
 29/02/2020
Giải giúp emTheo dõi (1) 12 Trả lời
29/02/2020
Giải giúp emTheo dõi (1) 12 Trả lời -


Tìm họ nguyên hàm của hàm số f(x)=3x^2-2x+5
bởi Dương Thị Ngân
 26/02/2020
26/02/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Xác định a, b, c sao cho hàm số F(x)=(ax^2+bx+c)e^-x là một nguyên hàm của hàm số f(x)=(2x^2-5x+2)e^-x
bởi Thanh Trà
 25/02/2020
25/02/2020

Giải giúp em với ạ
Theo dõi (0) 3 Trả lời -


Tìm nguyên hàm của (x^2/3+x^3/2)dx
bởi Trần Mai Linh
 25/02/2020
25/02/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm họ nguyên hàm của hàm số f(x)=e^x+x
bởi Thanh Tâm
 24/02/2020
24/02/2020
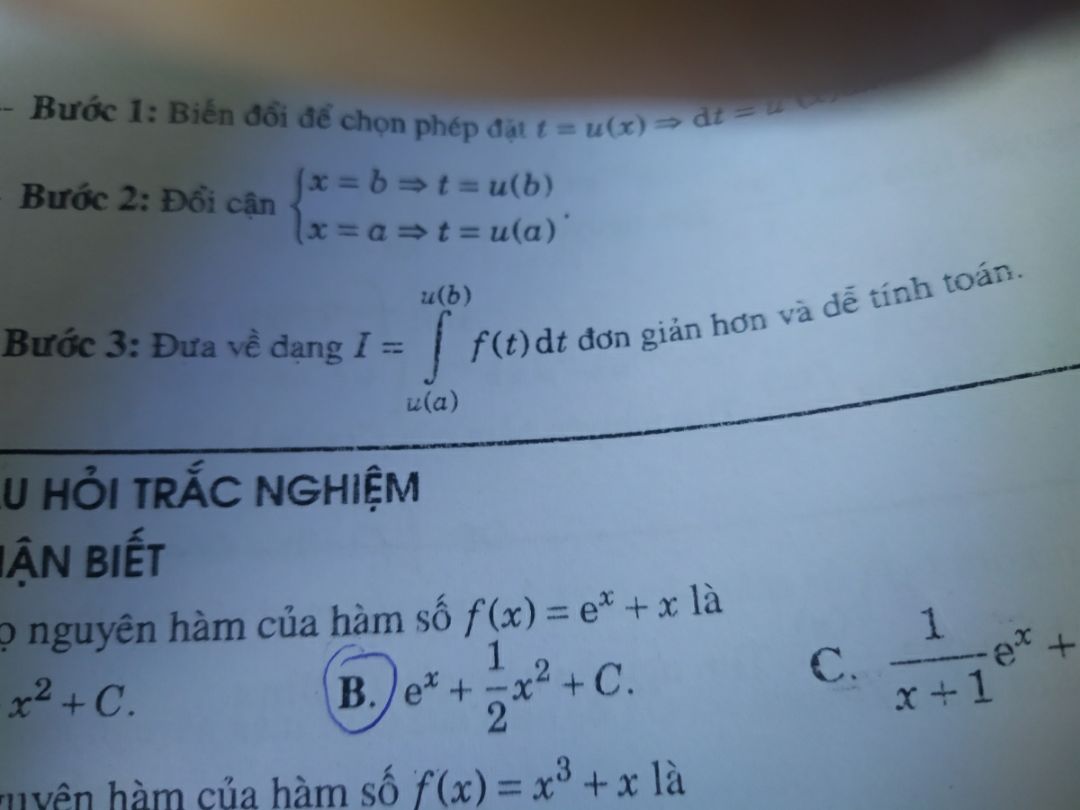 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tìm nguyên hàm của (cosx+sinx.cosx)/(2+sinx)dx
bởi Emmy Michael
 24/02/2020
24/02/2020
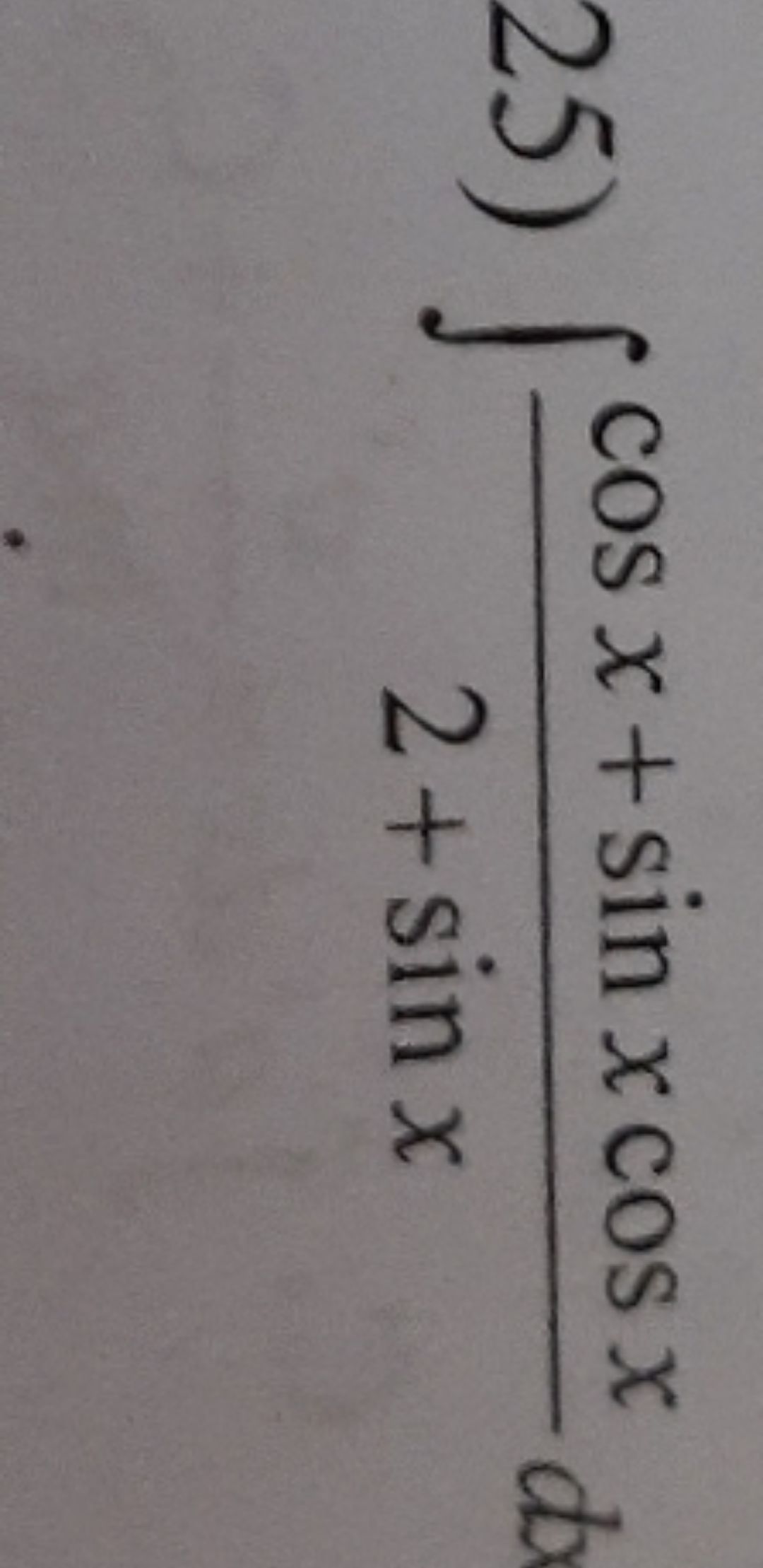 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm nguyên hàm của hàm số f(x)= sinx.cosx
bởi han pham van
 23/02/2020
Nguyên hàm của hs f(x)= sinxcosxTheo dõi (0) 3 Trả lời
23/02/2020
Nguyên hàm của hs f(x)= sinxcosxTheo dõi (0) 3 Trả lời -


Tìm họ nguyên hàm của hàm số f(x)=x-sin2x
bởi Võ Thị Ngọc Hà
 22/02/2020
22/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm nguyên hàm của x/cos^2 x?
bởi Nguyễn Quyên
 22/02/2020
22/02/2020
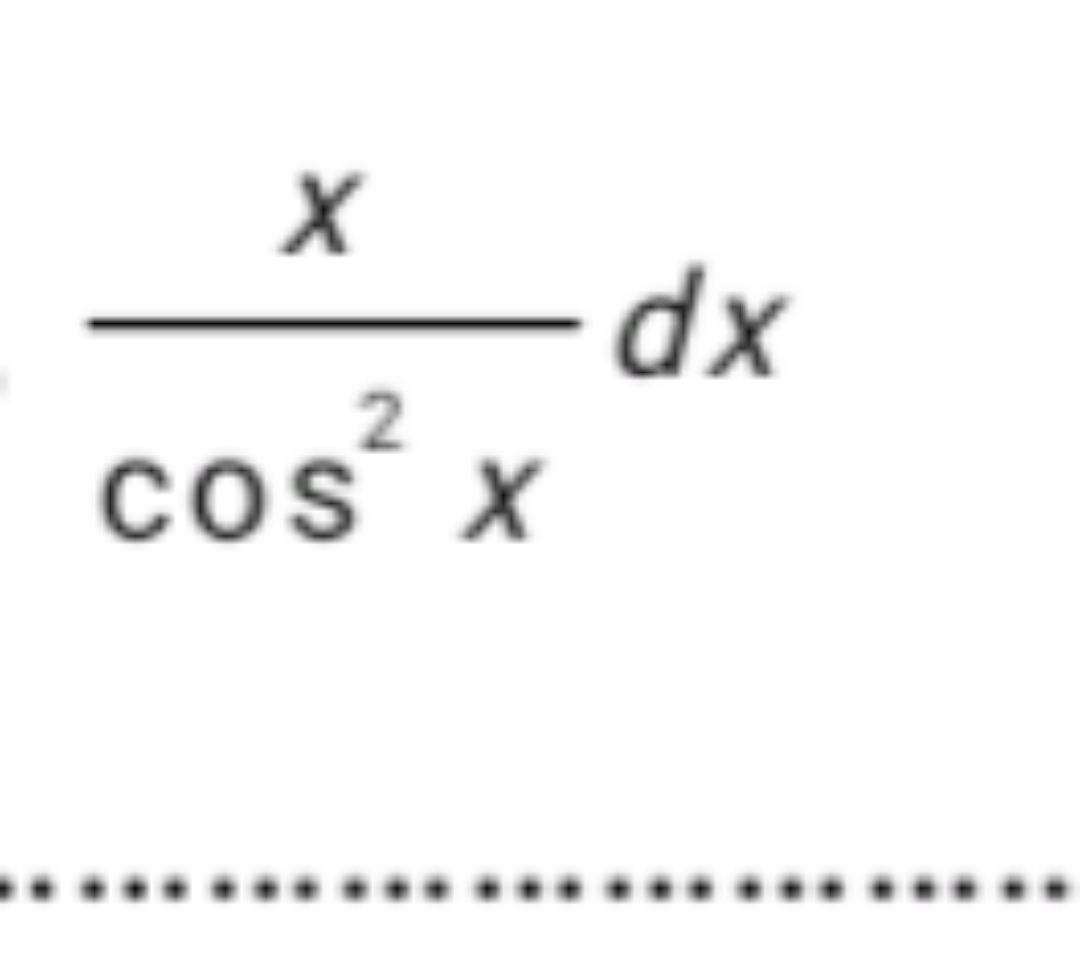 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm của x^4/(x^10-4)dx
bởi Quốc Khánh
 21/02/2020
hướng dẫn mình làm câu o với
21/02/2020
hướng dẫn mình làm câu o với Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời



