Phần hướng dẫn giải bài tập SGK Toán 9 Bài 4 Liên hệ giữa phép chia và phép khai phương sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 9 Tập một.
-
Bài tập 28 trang 18 SGK Toán 9 Tập 1
Tính:
a) \(\sqrt{\frac{289}{225}}\) b) \(\sqrt{2\frac{14}{25}}\)
c) \(\sqrt{\frac{0,25}{9}}\) d) \(\sqrt{\frac{8,1}{1,6}}\)
-
Bài tập 29 trang 19 SGK Toán 9 Tập 1
Tính
a) \(\frac{\sqrt{2}}{\sqrt{18}}\) b) \(\frac{\sqrt{15}}{\sqrt{735}}\)
c) \(\frac{\sqrt{12500}}{\sqrt{500}}\) d) \(\frac{\sqrt{6^{5}}}{\sqrt{2^{3}.3^{5}}}\)
-
Bài tập 30 trang 19 SGK Toán 9 Tập 1
Rút gọn các biểu thức sau:
a) \(\frac{y}{x}.\sqrt{\frac{x^{2}}{y^{4}}}\) với \(x > 0, y \neq 0\)
b) \(2y^2.\sqrt{\frac{x^{4}}{4y^{2}}}\) với \(y < 0\)
c) \(5xy.\sqrt{\frac{25x^{2}}{y^{6}}}\) với \(x < 0, y > 0\)
d) \(0,2x^{3}y^{3}.\sqrt{\frac{16}{x^{4}y^{8}}}\) với \(x\neq 0, y\neq 0\)
-
Bài tập 31 trang 19 SGK Toán 9 Tập 1
a) So sánh \(\sqrt{25 - 16}\) và \(\sqrt{25} - \sqrt{16}\);
b) Chứng minh rằng: với \(a > b >0\) thì \(\sqrt{a} - \sqrt{b} < \sqrt{a - b}\).
- VIDEOYOMEDIA
-
Bài tập 32 trang 19 SGK Toán 9 Tập 1
Tính
a) \(\sqrt{1\frac{9}{16}.5\frac{4}{9}.0,01}\) b) \(\sqrt{1,44.1,21-1,44.0,4}\)
c) \(\sqrt{\frac{165^{2}-124^{2}}{164}}\) d) \(\sqrt{\frac{149^{2}-76^{2}}{457^{2}-384^{2}}}\)
-
Bài tập 33 trang 19 SGK Toán 9 Tập 1
Giải phương trình
a) \(\sqrt{2}.x - \sqrt{50} = 0\) b) \(\sqrt{3}.x + \sqrt{3} = \sqrt{12} + \sqrt{27}\)
c) \(\sqrt{3}x^2-\sqrt{12}=0\) d) \(\frac{x^{2}}{\sqrt{5}}- \sqrt{20} = 0\)
-
Bài tập 34 trang 19 SGK Toán 9 Tập 1
Rút gọn các biểu thức sau:
a) \(ab^{2}.\sqrt{\frac{3}{a^{2}b^{4}}}\) với \(a < 0, b\neq 0\)
b) \(\sqrt{\frac{27(a - 3)^{2}}{48}}\) với \(a > 3\)
c) \(\sqrt{\frac{9+12a+4a^{2}}{b^{2}}}\) với \(a \geq -1,5;b<0\)
d) \((a - b).\sqrt{\frac{ab}{(a - b)^{2}}}\) với \(a < b < 0\)
-
Bài tập 35 trang 20 SGK Toán 9 Tập 1
Tìm x, biết:
a) \(\sqrt{(x-3)^{2}}=9\)
b) \(\sqrt{4x^{2}+4x+1}=6\)
-
Bài tập 36 trang 20 SGK Toán 9 Tập 1
Mỗi khẳng định sau đúng hay sai ? Vì sao ?
a) \(0,01=\sqrt{0,0001}\)
b)\(-0,5=\sqrt{-0,25}\)
c) \(\sqrt {39} < 7\) và \(\sqrt {39} >6\)
d) \((4-\sqrt{13})2x< \sqrt{3}(4-\sqrt{13})\Leftrightarrow 2x< \sqrt{3}\)
-
Bài tập 37 trang 20 SGK Toán 9 Tập 1
Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1cm, cho bốn điểm M, N, P, Q (h.3).
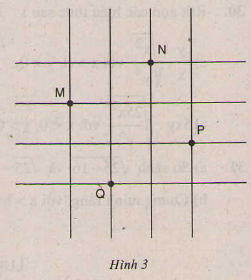
Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNPQ.
-
Bài tập 36 trang 10 SBT Toán 9 Tập 1
Áp dụng quy tắc khai phương một thương , hãy tính:
a) \(\sqrt {{9 \over {169}}} \);
b) \(\sqrt {{{25} \over {144}}} \);
c) \(\sqrt {1{9 \over {16}}} \);
d) \(\sqrt {2{7 \over {81}}} \).
-
Bài tập 37 trang 11 SBT Toán 9 Tập 1
Áp dụng quy tắc chia hai căn bậc hai, hãy tính:
a) \({{\sqrt {2300} } \over {\sqrt {23} }}\)
b) \({{\sqrt {12,5} } \over {\sqrt {0,5} }}\)
c) \({{\sqrt {192} } \over {\sqrt {12} }}\)
d) \({{\sqrt 6 } \over {\sqrt {150} }}\)
-
Bài tập 38 trang 11 SBT Toán 9 Tập 1
Cho các biểu thức:
A= \(\sqrt {{{2x + 3} \over {x - 3}}} \) và B = \({{\sqrt {2x + 3} } \over {\sqrt {x - 3} }}\)
a) Tìm x để A có nghĩa. Tìm x để B có nghĩa .
b) Với giá trị nào của x thì A=B ?
-
Bài tập 39 trang 11 SBT Toán 9 Tập 1
Biểu diễn \(\sqrt {{a \over b}} \) với a < 0 và b < 0 ở dạng thương của hai căn thức.
Áp dụng tính \(\sqrt {{{ - 49} \over { - 81}}} \)
-
Bài tập 40 trang 11 SBT Toán 9 Tập 1
Rút gọn các biểu thức:
a) \({{\sqrt {63{y^3}} } \over {\sqrt {7y} }}\) (y>0);
b) \({{\sqrt {48{x^3}} } \over {\sqrt {3{x^5}} }}\) (x > 0);
c) \({{\sqrt {45m{n^2}} } \over {\sqrt {20m} }}\) (m > 0 và n > 0);
d) \({{\sqrt {16{a^4}{b^6}} } \over {\sqrt {128{a^6}{b^6}} }}\) (a < 0 và b ≠ 0).
-
Bài tập 41 trang 11 SBT Toán 9 Tập 1
Rút gọn các biểu thức:
a) \(\sqrt {{{x - 2\sqrt x + 1} \over {x + 2\sqrt x + 1}}} \) (x ≥ 0);
b) \({{x - 1} \over {\sqrt y - 1}}\sqrt {{{{{(y - 2\sqrt y + 1)}^2}} \over {{{(x - 1)}^4}}}} \) (x ≠1, y ≠ 1 và y ≥ 0).
-
Bài tập 42 trang 12 SBT Toán 9 Tập 1
Rút gọn biểu thức với điều kiện đã cho của x rồi tính giá trị của nó:
a) \(\sqrt {{{{{(x - 2)}^4}} \over {{{(3 - x)}^2}}}} + {{{x^2} - 1} \over {x - 3}}\)
(x < 3); tại x = 0,5 ;
b) \(4x - \sqrt 8 + {{\sqrt {{x^3} + 2{x^2}} } \over {\sqrt {x + 2} }}\)
(x > -2); tại x = \( - \sqrt 2 \)
-
Bài tập 43 trang 12 SBT Toán 9 Tập 1
Tìm x thỏa mãn điều kiện
a) \(\sqrt {{{2x - 3} \over {x - 1}}} = 2\)
b) \({{\sqrt {2x - 3} } \over {\sqrt {x - 1} }} = 2\)
c) \(\sqrt {{{4x + 3} \over {x + 1}}} = 3\)
d) \({{\sqrt {4x + 3} } \over {\sqrt {x + 1} }} = 3.\)
-
Bài tập 44 trang 12 SBT Toán 9 Tập 1
Cho hai số a, b không âm. Chứng minh:
\({{a + b} \over 2} \ge \sqrt {ab} \)
(Bất đẳng thức Cô-si cho hai số không âm).
Dấu đẳng thức xảy ra khi nào ?
-
Bài tập 45 trang 12 SBT Toán 9 Tập 1
Với \( a ≥ 0, b ≥ 0\), chứng minh
\( \displaystyle\sqrt {{{a + b} \over 2}} \ge {{\sqrt a + \sqrt b } \over 2}.\)
-
Bài tập 46 trang 12 SBT Toán 9 Tập 1
Với a dương, chứng minh:
\(a + {1 \over a} \ge 2.\)
-
Bài tập 4.1 trang 12 SBT Toán 9 Tập 1
Giá trị của \(\sqrt {\dfrac{{49}}{{0,09}}} \) bằng
(A) \(\dfrac{7}{3}\);
(B) \(\dfrac{{70}}{3}\);
(C) \(\dfrac{7}{{30}}\);
(D) \(\dfrac{{700}}{3}\).
Hãy chọn đáp án đúng.





