Bài tập 44 trang 92 SGK Toán 8 Tập 1

Hướng dẫn giải chi tiết bài 44:

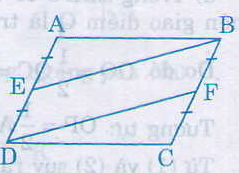
\(ABCD\) hình bình hành nên  \(DE // BF\) và \(AD=BC\)

\(E\) là trung điểm của \(AD\) (giả thiết) nên \(DE = \dfrac{1}{2}AD\) (tính chất trung điểm)

\(F\) là trung điểm của \(BC\) (giả thiết) nên \(BF= \dfrac{1}{2}BC\) (tính chất trung điểm)

Mà \(AD=BC\) (chứng minh trên) nên \(DE=BF\)

Tứ giác \(BEDF\) có \(DE//BF\) và \(DE=BF\) (chứng minh trên) 

\( \Rightarrow \) Tứ giác \(BEDF\) là hình bình hành (theo dấu hiệu nhận biết hình bình hành).

\( \Rightarrow \) \(BE = DF\) (tính chất hình bình hành).

Cách khác: 

+ \(ABCD\) là hình bình hành \(⇒ AB = CD, AD = BC, \widehat A=\widehat C.\)

+ \(E\) là trung điểm của \(AD\) \( ⇒ AE = \dfrac{1}{2}AD\) (tính chất trung điểm)

\(F\) là trung điểm của \(BC \) \(⇒ BF= \dfrac{1}{2}BC\) (tính chất trung điểm)

Mà \(AD = BC\) (chứng minh trên) \(⇒ AE = CF\)

+ Xét \(ΔAEB\) và \(ΔCFD\) có: \(AB = CD, \widehat A=\widehat C, AE = CF\) (chứng minh trên)

\(⇒ ΔAEB = ΔCFD (c.g.c)\)

\(⇒ EB = DF.\)

-- Mod Toán 8 HỌC247