Giải bài 77 tr 89 sách BT Toán lớp 8 Tập 1
Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Vì sao ?
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Lời giải chi tiết
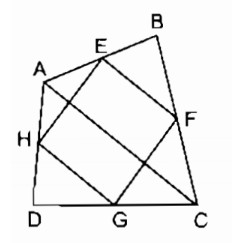
Nối đường chéo AC.
Trong ∆ ABC ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
nên EF là đường trung bình của ∆ ABC
⇒ EF // AC và EF \( = {1 \over 2}\)AC (tính chất đường trung bình tam giác) (1)
Trong ∆ ADC ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
nên HG là đường trung bình của ∆ ADC
⇒ HG // AC và HG \( = {1 \over 2}\)AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 75 trang 89 SBT Toán 8 Tập 1
Bài tập 76 trang 89 SBT Toán 8 Tập 1
Bài tập 78 trang 89 SBT Toán 8 Tập 1
Bài tập 79 trang 89 SBT Toán 8 Tập 1
Bài tập 80 trang 89 SBT Toán 8 Tập 1
Bài tập 81 trang 90 SBT Toán 8 Tập 1
Bài tập 82 trang 90 SBT Toán 8 Tập 1
Bài tập 83 trang 90 SBT Toán 8 Tập 1
Bài tập 84 trang 90 SBT Toán 8 Tập 1
Bài tập 85 trang 90 SBT Toán 8 Tập 1
Bài tập 86 trang 90 SBT Toán 8 Tập 1
Bài tập 87 trang 90 SBT Toán 8 Tập 1
Bài tập 88 trang 90 SBT Toán 8 Tập 1
Bài tập 89 trang 91 SBT Toán 8 Tập 1
Bài tập 90 trang 91 SBT Toán 8 Tập 1
Bài tập 91 trang 91 SBT Toán 8 Tập 1
Bài tập 7.1 trang 91 SBT Toán 8 Tập 1
-


Chứng minh BMNP là hình bình hành biết tam giác ABC có M, N, P là trung điểm của AB, AC, BC
bởi Nguyễn Sơn Ca
 31/05/2019
31/05/2019
cho tam giac ABC.Goi M,N,P lan luot la trung diem AB,AC,BC.CM:tu giac BMNP la hinh binh hanh.
Ve hinh ,giai chi tiet.
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác BHCD là hình bình hành biết tam giác ABC có đườnh cao BM cắt CN tại H
bởi Anh Trần
 31/05/2019
31/05/2019
Cho tam giác ABC . Đường cao BM cắt CN tại H .D đối xứng với H qua trung điểm O của BC
Cm tứ giác BHCD là hình bình hành
Cm tứ giác BMCD là hình thang vuông
Theo dõi (0) 1 Trả lời -


Chứng minh AECF là hình bình hành biết hình bình hành có AE, CF lần lượt vuông góc với BD
bởi sap sua
 31/05/2019
31/05/2019
Cho hình bình hành ABCD.Kẻ AE vuông góc BD,kẻ CF vuông góc với BD.
a, Tứ giác AECF là hình gì? Vì sao/
b, AE cắt CD ở I, CF cắt AB ở K. CM: AI=CK
c, CM: BE=DF
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho AD là phân giác của \(\Delta ABC\).Qua D kẻ đường thẳng Dx // AB, Dx cắt cạnh AC tại điểm E. Vẽ đường thẳng Ey // BC, Ey cắt cạnh AB tại điểm F. Chứng tỏ rằng : AE = BF
Theo dõi (0) 1 Trả lời -


tính để biểu thức 9x^2 + 30x + a là bình phương của một tổng
Theo dõi (0) 1 Trả lời -


Rút gọn 6x - 2y / 3x^2 - xy
bởi ngọc trang
 31/05/2019
31/05/2019
rút gọn
6x - 2y / 3x^2 - xyTheo dõi (0) 1 Trả lời





