Giải bài 83 tr 90 sách BT Toán lớp 8 Tập 1
Cho hình bình hành \(ABCD.\) Gọi \(E,\) \(F\) theo thứ tự là trung điểm của \(AB,\) \(CD.\) Gọi \(M\) là giao điểm của \(AF\) và \(DE,\) \(N\) là giao điểm của \(BF\) và \(CE.\) Chứng minh rằng :
\(a)\) \(EMFN\) là hình bình hành.
\(b)\) Các đường thẳng \(AC,\) \(EF,\) \(MN\) đồng quy.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Trong hình bình hành, các cạnh đối bằng nhau.
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết
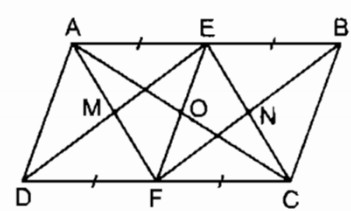
Vì ABCD là hình bình hành nên \(AB//CD\) và \(AB=CD\) (tính chất)
Ta có: \(AE = EB = \dfrac{{AB}}{2}\) (vì E là trung điểm của AB)
\(DF= CF = \dfrac{{DC}}{2}\) (vì F là trung điểm của CD)
Mà \(AB=CD\) (cmt)
Suy ra \(AE=EB=DF=FC\)
Xét tứ giác \(AECF,\) có:
\(AE = CF\) (cmt)
\(AE // CF\) (do \(AB // CD\;)\)
Suy ra tứ giác \(AECF\) là hình bình hành ( vì có một cặp cạnh đối diện song song và bằng nhau)
\(⇒ AF // CE\) hay \(EN // FM \;\;(1)\)
Xét tứ giác \(BFDE,\) có:
\(BE = DF\) (cmt)
\(BE // DF\) (do \(AB // CD\))
Suy ra tứ giác \(BFDE\) là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
\(⇒ BF // DE\) hay \(EM // FN \;\;(2)\)
Từ \((1)\) và \((2)\) suy ra tứ giác \(EMFN\) là hình bình hành (theo định nghĩa)
\(b)\) Gọi \(O\) là giao điểm của \(AC\) và \(EF\)
Tứ giác \(AECF\) là hình bình hành \(⇒ OE = OF\)
Tứ giác \(EMFN\) là hình bình hành nên hai đường chéo cắt nhau tại trung điểm mỗi đường.
Suy ra: \(MN\) đi qua trung điểm \(O\) của \(EF\)
Vậy \(AC, EF, MN \) đồng quy tại \(O.\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 81 trang 90 SBT Toán 8 Tập 1
Bài tập 82 trang 90 SBT Toán 8 Tập 1
Bài tập 84 trang 90 SBT Toán 8 Tập 1
Bài tập 85 trang 90 SBT Toán 8 Tập 1
Bài tập 86 trang 90 SBT Toán 8 Tập 1
Bài tập 87 trang 90 SBT Toán 8 Tập 1
Bài tập 88 trang 90 SBT Toán 8 Tập 1
Bài tập 89 trang 91 SBT Toán 8 Tập 1
Bài tập 90 trang 91 SBT Toán 8 Tập 1
Bài tập 91 trang 91 SBT Toán 8 Tập 1
Bài tập 7.1 trang 91 SBT Toán 8 Tập 1
-


?2Hình thang ABCD có đáy AB, CD
a) cho biết AD//BC. Chứng minh AD=BC; AB=CD
b)Cho biết AB=CD. Chứng minh rằng AD//BC,AD=BC
các bạn vẽ hình giùm mình nha!
thank you!
Theo dõi (0) 1 Trả lời -


Tính chu vi hình bình hành MNPQ biết M,N,P,Q là trung điểm của các cạnh BD, AB,AC,CD
bởi Phạm Khánh Linh
 31/05/2019
31/05/2019
Cho tứ giác ABCD. Gọi M,N,P,Q lần lượt là trung điểm của các cạnh BD, AB,AC,CD
a, cmr tứ giác MNPQ là hình bình hành
b, cho AD=a, BC=b. Tính chu vi hình bình hành MNPQ
Theo dõi (0) 1 Trả lời -


Chứng minh AMNC là hình thang biết hình thang ABCD có M, N là trung điểm OB, OD
bởi Huong Duong
 31/05/2019
31/05/2019
Cho hình bình hành ABCD, O là giao điểm 2 đường chéo AC,BD.M,N là trung điểm OB,OD
a) CMR AMNC là hình thang
b) tia AM cắt BC ở E
Theo dõi (0) 1 Trả lời -


Chứng minh F và K đối xứng với nhau qua điểm A
bởi Lê Minh Hải
 31/05/2019
31/05/2019
cho tam giác MNP lấy điểm E thuộc NP kẻ EF//MN , F thuộc MP kẻ EK//MP , K thuộc MN . Gọi A là trung điểm của ME . Chứng minh rằng : F và K đối xứng với nhau qua điểm A
LÀM ƠN GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh tứ giác AECF là hình bình hành biết hình bình hành ABCD có 2 đường chéo cắt nhau tại O
bởi Nguyễn Minh Hải
 31/05/2019
31/05/2019
Cho hình bình hành ABCD. Hai đường chéo AC và BD cắt nhau tại O. Từ A và C vẽ các đường thẳng vẽ các đường thẳng vuông góc với AE, CF xuống BD ( E, F thuộc BD)
a) so sánh OE và OF
b) chứng minh: tứ giác AECF là hình bình hành
Theo dõi (0) 1 Trả lời -


CM nếu tứ giac có đường chéo và các đoạn thẳng nối trung điểm các cặp cạnh đối đồng quy thì tứ giác là hình bình hành
bởi Nguyễn Vũ Khúc
 31/05/2019
31/05/2019
Chứng minh rằng: Nếu một tứ giác có các đường chéo và các đoạn thẳng nối trung điểm của các cặp cạnh đối đồng quy thì tứ giác đó là một hình bình hành
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông tại A , AH vuông với BC ( H thuộc BC) . điểm E đối xứng với H qua AB , điểm F đối xứng với H qua AC . AB cắt EH tại M , AC cắt HF tại N
a) tứ giác AMHN là hình gì ? vì sao
b) E đối xứng với F qua A
c) kẻ trung tuyến AI của tam giác ABC . c/m AI vuông với MNTheo dõi (0) 1 Trả lời






