Giải bài 84 tr 90 sách BT Toán lớp 8 Tập 1
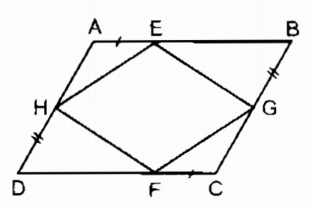
Trên hình 11, cho ABCD là hình bình hành. Chứng minh rằng:
a. EGFH là hình bình hành
b. Các đường thẳng AC, BD, EF, GH đồng quy.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Trong hình bình hành, hai góc đối bằng nhau.
+) Tứ giác có các cạnh đối bằng nhau là hình bình hành.
+) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết
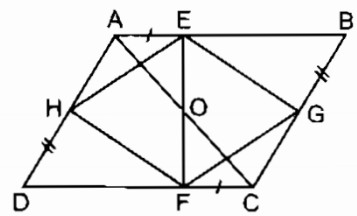
a. Xét ∆ AEH và ∆ CFG:
AE = CF
\(\widehat A = \widehat C\) (tính chất hình bình hành)
AH = CG (vì AD = BC và DH = BG)
Do đó: ∆ AEH = ∆ CFG (c.g.c)
⇒ EH = FG
Xét ∆ BEG và ∆DFH:
DH = BG (gt)
\(\widehat B = \widehat D\) (tính chất hình bình hành)
BE = DF (vì AB = CD và AE = CF)
Do đó: ∆ BEG = ∆DFH (c.g.c)
⇒ EG = FH
Suy ra: Tứ giác EGFH là hình bình hành (vì có cắc cặp cạnh đối bằng nhau)
b. Gọi O là giao điểm của AC và EF.
Xét tứ giác AECF:
AB // CD (gt) hay AE // CF
AE = CF (gt)
Suy ra: Tứ giác AECF là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau)
⇒ O là trung điểm của AC và EF
Tứ giác ABCD là hình bình hành có O là trung điểm của AC nên O cũng là trung điểm của BD.
Tứ giác EGFH là hình bình hành có O là trung điểm của EF nên O cùng là trung điểm của GH.
Vậy AC, BD, GH đồng quy tại O.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 82 trang 90 SBT Toán 8 Tập 1
Bài tập 83 trang 90 SBT Toán 8 Tập 1
Bài tập 85 trang 90 SBT Toán 8 Tập 1
Bài tập 86 trang 90 SBT Toán 8 Tập 1
Bài tập 87 trang 90 SBT Toán 8 Tập 1
Bài tập 88 trang 90 SBT Toán 8 Tập 1
Bài tập 89 trang 91 SBT Toán 8 Tập 1
Bài tập 90 trang 91 SBT Toán 8 Tập 1
Bài tập 91 trang 91 SBT Toán 8 Tập 1
Bài tập 7.1 trang 91 SBT Toán 8 Tập 1
-


Chứng minh H,O,K thẳng hàng biết hình bình hành ABCD có AH, CK vuông góc với đường chéo BD
bởi thu hằng
 31/05/2019
31/05/2019
Cho hình bình hành ABCD, Kẻ AH; Ck vuông góc với đường chéo BD:
a) CM AHCK là hình bình hành
b) Gọi O là giao điểm của AC và BD. CHứng tỏ H,O,K thẳng hàng.
Theo dõi (0) 1 Trả lời -


choΔABC (AB<AC.AH là dường cao .kẻ MNP lần lượt là trung điểm cac cạnhAB,AC,BC
CMː BCNM là hbh
MNPB là hình thoi
HPNM là hình thang cân
⇔giúp mình nha cần ∞
Theo dõi (0) 1 Trả lời -


a.Cho tứ giác ABCD biết AB//CD và AB=CD.CMR AD//BC và AD=BC
b.Cho tứ giác ABCD biết AB//CD và AD//BC.CMR:AB=CD và AD=BC
c.Cho tứ giác ABCD biết AB=CD và AD=BC.CMR AD//BC và AD//BC
help me!!
Theo dõi (0) 1 Trả lời -


Chứng minh EFGH là hình bình hành biết tứ giác ABCD gọi E, F, G, H theo thứ tự là trung điểm của BD, AB, AC, CD
bởi Tra xanh
 31/05/2019
31/05/2019
Cho tứ giác ABCD gọi E, F, G, H theo thứ tự là trung điểm của BD, AB, AC, CD.
a) Chứng minh EFGH là hình bình hành.
b) Cho AD = a, BC = b, tình chu vi hình bình hành EFGH ?Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng min tứ giác AMCN là hình bình hành biết hình bình hành ABCD có M, N là trung điểm của AD, BC
bởi Mai Đào
 31/05/2019
31/05/2019
cho hình bình hành ABCD . M ,N lần lượt là trung điểm của AD,BC
a, chứng minh tứ giác AMCN là hình bình hành
b, chứng minh tứ giác BMDN là hình bình hành
Theo dõi (0) 1 Trả lời -


Chứng minh MHPK là hình bình hành biết trên đường chéo NQ lấy các điểm H và K sao cho NH=HK=KQ
bởi Mai Hoa
 31/05/2019
31/05/2019
cho hình bình hành MNPQ. Trên đường chéo NQ lấy các điểm H và K sao cho NH=HK=KQ.
a) chứng minh rằng MHPK là hình bình hành
b) Trên tia đối của tia MN, NP, PQ và QM lần lượt lấy A, B, C, D sao cho AM=BN=CP=DQ. chứng minh rằng MP, HK, AC, BD đồng quy
Theo dõi (0) 1 Trả lời -


Chứng minh AHCK là hình bình hành biết hình bình hành ABCD có AH vuông góc với BD
bởi Lan Anh
 31/05/2019
31/05/2019
bài 1 :cho hình bình hành ABCD . Kẻ AH và CK vuông góc với BD
a) Chứng minh :AHCK là hình bình hành
b)Gọi O là trung điểm của AC . Chứng minh H đối xứng với K qua O
Bài 2 :cho tứ giác ABCD gọi M , N , P , Q là trung điểm của AB ,BC , CD ,DA .
Chứng minh MNPQ là hình bình hành
Theo dõi (0) 1 Trả lời





