Giải bài 47 tr 93 sách GK Toán 8 Tập 1
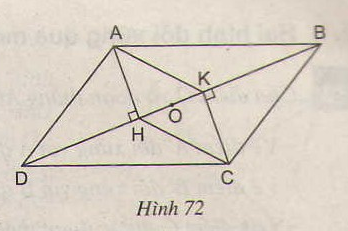
Cho hình 72, trong đó ABCD là hình bình hành.
a) Chứng minh rằng AHCK là hình bình hành.
b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng
Hướng dẫn giải chi tiết
Câu a:
Xét hai tam giác vuông \(AHD\) và \(CKB\) có:
+) \( AD = CB\) (vì \(ABCD\) là hình bình hành)
+) \(\widehat {ADH} = \widehat {CBK}\) (hai góc ở vị trí so le trong, \(AD//BC\))
\( \Rightarrow \) \(∆AHD = ∆CKB\) (cạnh huyền- góc nhọn)
\( \Rightarrow \) \(AH = CK\) (\(2\) cạnh tương ứng)
Ta có:
\(\left\{ \begin{array}{l}
AH \bot B{\rm{D}}\\
CK \bot B{\rm{D}}
\end{array} \right.\left( \text{giả thiết} \right) \Rightarrow AH//CK\)
Xét tứ giác \(AHCK\) có:
\(\left\{ \begin{array}{l}
AH//CK\\
AH = CK
\end{array} \right.\left( \text{chứng minh trên} \right)\)
\( \Rightarrow \) tứ giác \(AHCK\) là hình bình hành (dấu hiệu nhận biết hình bình hành).
Câu b:
Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 45 trang 92 SGK Toán 8 Tập 1
Bài tập 46 trang 92 SGK Toán 8 Tập 1
Bài tập 48 trang 93 SGK Toán 8 Tập 1
Bài tập 49 trang 93 SGK Toán 8 Tập 1
Bài tập 73 trang 89 SBT Toán 8 Tập 1
Bài tập 74 trang 89 SBT Toán 8 Tập 1
Bài tập 75 trang 89 SBT Toán 8 Tập 1
Bài tập 76 trang 89 SBT Toán 8 Tập 1
Bài tập 77 trang 89 SBT Toán 8 Tập 1
Bài tập 78 trang 89 SBT Toán 8 Tập 1
Bài tập 79 trang 89 SBT Toán 8 Tập 1
Bài tập 80 trang 89 SBT Toán 8 Tập 1
Bài tập 81 trang 90 SBT Toán 8 Tập 1
Bài tập 82 trang 90 SBT Toán 8 Tập 1
Bài tập 83 trang 90 SBT Toán 8 Tập 1
Bài tập 84 trang 90 SBT Toán 8 Tập 1
Bài tập 85 trang 90 SBT Toán 8 Tập 1
Bài tập 86 trang 90 SBT Toán 8 Tập 1
Bài tập 87 trang 90 SBT Toán 8 Tập 1
Bài tập 88 trang 90 SBT Toán 8 Tập 1
Bài tập 89 trang 91 SBT Toán 8 Tập 1
Bài tập 90 trang 91 SBT Toán 8 Tập 1
Bài tập 91 trang 91 SBT Toán 8 Tập 1
Bài tập 7.1 trang 91 SBT Toán 8 Tập 1
-


Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu sai.
bởi Nguyen Nhan
 15/01/2021
15/01/2021
A. BH // CD
B. CH // BD
C. BH = CD
D. HB = HC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC và H là trực tâm. Các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C cắt nhau ở D. Chọn câu trả lời đúng nhất. Tứ giác BDCH là hình gì?
bởi thu thủy
 15/01/2021
15/01/2021
A. Hình thang
B. Hình bình hành
C. Hình thang cân
D. Hình thang vuông
Theo dõi (0) 1 Trả lời -


Cho hình bình hành ABCD. Tia phân giác của góc A cắt CD tại M. Tia phân giác góc C cắt AB tại N (hình vẽ). Hãy chọn câu trả lời sai.
bởi Van Dung
 16/01/2021
16/01/2021
.png)
A. AMCN là hình bình hành
B. CMBA là hình thang
C. ANCD là hình thang cân
D. AN = MC
Theo dõi (0) 1 Trả lời -


Hãy chọn câu trả lời sai. Cho hình vẽ, ta có:
bởi Lam Van
 15/01/2021
15/01/2021
.png)
A. ABCD là hình bình hành
B. AB // CD
C. ABCE là hình thang cân
D. BC // AD
Theo dõi (0) 1 Trả lời -
ADMICRO


Hãy chọn câu đúng. Cho hình bình hành ABCD, gọi E là trung điểm của AB, F là trung điểm của CD. Khi đó:
bởi Thanh Nguyên
 16/01/2021
16/01/2021
A. DE = BF
B. DE > BF
C. DE < BF
D. DE = EB
Theo dõi (0) 1 Trả lời -


Hãy chọn câu đúng. Cho hình bình hành ABCD có các điều kiện như hình vẽ, trong hình có:
bởi Hoa Hong
 15/01/2021
15/01/2021
.png)
A. 6 hình bình hành
B. 5 hình bình hành
C. 4 hình bình hành
D. 3 hình bình hành
Theo dõi (0) 1 Trả lời -


Hãy chọn câu đúng. Tứ giác ABCD là hình bình hành nếu.
bởi Phung Hung
 15/01/2021
15/01/2021
A. \(\widehat A = \widehat C\)
B. AB = CD, BC = AD
C. AB // CD
D. BC = AD
Theo dõi (0) 1 Trả lời





