Phß║ºn hã░ß╗øng dß║½n giß║úi b├ái tß║¡p SGK To├ín 9 B├ái 1 Nhß║»c lß║íi v├á bß╗ò sung c├íc kh├íi niß╗çm vß╗ü h├ám sß╗æ sß║¢ gi├║p c├íc em nß║»m ─æã░ß╗úc phã░ãíng ph├íp v├á r├¿n luyß╗çn k─® n─âng c├íc dß║íng b├ái tß║¡p tß╗½ SGK To├ín 9 Tß║¡p mß╗Öt.
-
Bài tập 1 trang 44 SGK Toán 9 Tập 1
a) Cho hàm số \(y = f(x) = \frac{2}{3} x\)
Tính: \(f(-2); f(-1); f(0); f(\frac{1}{2}); f(1); f(2); f(3)\)
b) Cho hàm số \(y = g(x) = \frac{2}{3} x + 3\)Tính: \(g(-2); g(-1); g(0); g(\frac{1}{2}); g(1); g(2); g(3)\)
c) C├│ nhß║¡n x├®t g├¼ vß╗ü gi├í trß╗ï cß╗ºa hai h├ám sß╗æ ─æ├ú cho ß╗ƒ tr├¬n khi biß║┐n x lß║ºy c├╣ng mß╗Öt gi├í trß╗ï ?
-
Bài tập 2 trang 45 SGK Toán 9 Tập 1
Cho hàm số \(y = - \frac{1}{2}x + 3\)
a) T├¡nh c├íc gi├í trß╗ï tã░ãíng ß╗®ng cß╗ºa y theo c├íc gi├í trß╗ï cß╗ºa x rß╗ôi ─æiß╗ün v├áo bß║úng sau:
b) Hàm số đã cho là hàm số đồng biến hay nghịch biến ? Vì sao ?
-
Bài tập 3 trang 45 SGK Toán 9 Tập 1
Cho hai hàm số y = 2x và y = -2x.
a) Vß║¢ tr├¬n c├╣ng mß╗Öt mß║Àt phß║│ng tß╗ìa ─æß╗Ö ─æß╗ô thß╗ï cß╗ºa hai h├ám sß╗æ ─æ├ú cho.
b) Trong hai hàm số đã cho, hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
-
Bài tập 4 trang 45 SGK Toán 9 Tập 1
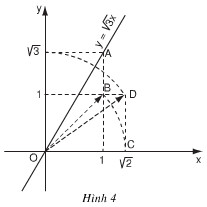
─Éß╗ô thß╗ï h├ám sß╗æ \(y = \sqrt{3} x\) ─æã░ß╗úc vß║¢ bß║▒ng compa v├á thã░ß╗øc thß║│ng ß╗ƒ h├¼nh 4
H├úy t├¼m hiß╗âu v├á tr├¼nh b├áy lß║íi c├íc bã░ß╗øc thß╗▒c hiß╗çn vß║¢ ─æß╗ô thß╗ï ─æ├│.
- VIDEOYOMEDIA
-
Bài tập 5 trang 45 SGK Toán 9 Tập 1
a) Vß║¢ ─æß╗ô thß╗ï h├ám sß╗æ \(y = x\) v├á \(y = 2x\) tr├¬n c├╣ng mß╗Öt mß║Àt phß║│ng tß╗ìa ─æß╗Ö Oxy (h.5).
b) ─Éã░ß╗Øng thß║│ng song song vß╗øi trß╗Ñc Ox v├á cß║»t trß╗Ñc Oy tß║íi ─æiß╗âm c├│ tung ─æß╗Ö \(y = 4\) lß║ºn lã░ß╗út cß║»t c├íc ─æã░ß╗Øng thß║│ng \(y = 2x\), \(y = x\) tß║íi hai ─æiß╗âm A v├á B.
T├¼m tß╗ìa ─æß╗Ö cß╗ºa c├íc ─æiß╗âm A, B v├á t├¡nh chu vi, diß╗çn t├¡ch cß╗ºa tam gi├íc OAB theo ─æãín vß╗ï ─æo tr├¬n c├íc trß╗Ñc tß╗ìa ─æß╗Ö l├á xentim├®t.

-
Bài tập 6 trang 45 SGK Toán 9 Tập 1
Cho các hàm số \(y = 0,5x\) và \(y = 0,5x + 2\)
a) T├¡nh gi├í trß╗ï y tã░ãíng ß╗®ng vß╗øi mß╗ùi h├ám sß╗æ theo gi├í trß╗ï ─æ├ú cho cß╗ºa biß║┐n x rß╗ôi ─æiß╗ün v├áo bß║úng sau:
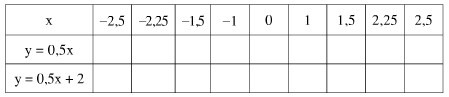
b) C├│ nhß║¡n x├®t g├¼ vß╗ü c├íc gi├í trß╗ï tã░ãíng ß╗®ng cß╗ºa hai h├ám sß╗æ ─æ├│ khi biß║┐n x lß║Ñy c├╣ng mß╗Öt gi├í trß╗ï?
-
Bài tập 7 trang 46 SGK Toán 9 Tập 1
Cho hàm số y = f(x) = 3x.
Cho x hai giá trị bất kì x1, x2 sao cho x1 < x2 .
H├úy chß╗®ng minh f(x1) < f(x2) rß╗ôi r├║t ra kß║┐t luß║¡n h├ám sß╗æ ─æ├ú cho ─æß╗ông biß║┐n tr├¬n R.
-
Bài tập 1 trang 60 SBT Toán 9 Tập 1
Trong c├íc bß║úng sau ghi c├íc gi├í trß╗ï tã░ãíng ß╗®ng cß╗ºa x v├á y. Bß║úng n├áo x├íc ─æß╗ïnh y l├á h├ám sß╗æ cß╗ºa x? V├¼ sao?
a)
x 1 2 4 5 7 8 y 3 5 9 11 15 17 b)
x 3 4 3 5 8 y 6 8 4 8 16 -
Bài tập 2 trang 60 SBT Toán 9 Tập 1
Cho hàm số y = f(x) = 1,2x
T├¡nh c├íc gi├í trß╗ï tã░ãíng ß╗®ng cß╗ºa y khi cho x c├íc gi├í trß╗ï sau ─æ├óy, rß╗ôi lß║¡p bß║úng c├íc gi├í trß╗ï tã░ãíng ß╗®ng giß╗»a x v├á y:
-2,5 -2,25 -2 -1,75 -1,5 -1,25 -1 -0,75 -0,5 -0,25 0 0,25 0,5 0,75 1 1,25 1,5 1,75 2 2,25 2,5 -
Bài tập 3 trang 60 SBT Toán 9 Tập 1
Cho hàm số y = f(x) = \(\frac{3}{4}x\). Tính:
f(-5) f(-4) f(-1) f(0) f(1/2 ) f(1) f(2) f(4) f(a) f(a + 1) -
Bài tập 4 trang 60 SBT Toán 9 Tập 1
Cho h├ám sß╗æ y = f(x) = \(\frac{2}{3}x\) + 5 vß╗øi x Ôêê R. Chß╗®ng minh rß║▒ng h├ám sß╗æ ─æß╗ông biß║┐n tr├¬n R.
-
Bài tập 5 trang 61 SBT Toán 9 Tập 1
Biß╗âu diß╗àn c├íc ─æiß╗âm sau ─æ├óy tr├¬n c├╣ng mß╗Öt hß╗ç trß╗Ñc tß╗ìa ─æß╗Ö. Nß╗æi theo thß╗® tß╗▒ c├íc ─æiß╗âm ─æ├ú cho bß║▒ng c├íc ─æoß║ín thß║│ng ─æß╗â ─æã░ß╗úc mß╗Öt ─æã░ß╗Øng gß║Ñp kh├║c vß╗øi ─æiß╗âm ─æß║ºu l├á A, ─æiß╗âm cuß╗æi l├á M.
A(1; 6) B(6; 11) C(14; 12) D(12; 9) E(15; 8) F(13; 4) G(9; 7) H(12; 1) I(16; 4) K(20; 1) L(19; 9) M(22; 6) -
Bài tập 6 trang 61 SBT Toán 9 Tập 1
Biß╗âu diß╗àn c├íc ─æiß╗âm sau ─æ├óy tr├¬n c├╣ng mß╗Öt hß╗ç trß╗Ñc tß╗ìa ─æß╗Ö. Nß╗æi theo thß╗® tß╗▒ c├íc ─æiß╗âm ─æ├ú cho bß║▒ng c├íc ─æoß║ín thß║│ng ─æß╗â ─æã░ß╗úc mß╗Öt ─æã░ß╗Øng gß║Ñp kh├║c vß╗øi ─æiß╗âm ─æß║ºu l├á A, ─æiß╗âm cuß╗æi l├á M.
A(1; 6) B(6; 11) C(14; 12) D(12; 9) E(15; 8) F(13; 4) G(9; 7) H(12; 1) I(16; 4) K(20; 1) L(19; 9) M(22; 6) -
Bài tập 1.1 trang 61 SBT Toán 9 Tập 1
Cho 4 bß║úng ghi c├íc gi├í trß╗ï tã░ãíng ß╗®ng cß╗ºa x v├á y (h.bs.1)
Bảng 1
x 0,5 1 1,5 0,5 2 2,5 y 2,5 3 4,5 3,5 5 6,5 Bảng 2
x -1 -2 1 1,5 1,5 2 y 3 5 3 2 1 5 Bảng 3
x 0 1 1,5 2 2,5 3 y 0 2 3 4 5 6 Bảng 4
x -1 2 -1 3 4 5 y -2 3 2 5,5 6,5 8,5 Trong các bảng trên đây, bảng xác định y là hàm số của x là:
A. Bảng 1; B. Bảng 2; C. Bảng 3; D. Bảng 4.
-
Bài tập 1.2 trang 61 SBT Toán 9 Tập 1
Cho h├ám sß╗æ y = f(x) = 4 - 2/5x vß╗øi x Ôêê R. Chß╗®ng minh rß║▒ng h├ám sß╗æ ─æ├ú cho nghß╗ïch biß║┐n tr├¬n R.
-
Bài tập 1 trang 60 SBT Toán 9 Tập 1
Trong ca╠üc ba╠ëng sau ghi ca╠üc gia╠ü tri╠ú tã░ãíng ã░╠üng cß╗ºa x va╠Ç y. Ba╠ëng na╠Ço xa╠üc ─æi╠únh y la╠Ç ha╠Çm s├┤╠ü cu╠ëa x? Vi╠Ç sao?
a.
x
1
2
4
5
7
8
Y
3
5
9
11
15
17
b.
x
3
4
3
5
8
y
6
8
4
8
16
-
Bài tập 2 trang 60 SBT Toán 9 Tập 1
Cho ha╠Çm s├┤╠ü \(y = f\left( x \right) = 1,2x\). Ti╠ünh ca╠üc gia╠ü tri╠ú tã░ãíng ã░╠üng cu╠ëa y khi cho x ca╠üc gia╠ü tri╠ú sau ─æ├óy, r├┤╠Çi l├ó╠úp ba╠ëng gia╠ü tri╠ú tã░ãíng ã░╠üng giã░╠âa \(x\) va╠Ç \(y\):
\(-2,50\); \(-2,25\); \(-2,00\); \(-1,75\); \(-1,50\); \(-1,25\); \(-1\);
\(-0,75\); \(-0,50\); \(-0,25\); \(0\); \(0,25\); \(0,05\); \(0,75\);
\(1\); \(1,25\); \(1,50\); \(1,75\) ; \(2,00\); \(2,25\); \(2,50.\)
-
Bài tập 3 trang 60 SBT Toán 9 Tập 1
Cho hàm số \(y = f\left( x \right) = \dfrac{3}{4}x\). Tính
\(f\left( { - 5} \right)\); \(f\left( { - 4} \right)\); \(f\left( { - 1} \right)\); \(f\left( 0 \right)\); \(f\left( {\dfrac{1}{2}} \right)\);
\(f\left( 1 \right)\); \(f\left( 2 \right)\); \(f\left( 4 \right)\); \(f\left( a \right)\); \(f\left( {a + 1} \right)\).
-
Bài tập 4 trang 60 SBT Toán 9 Tập 1
Cho ha╠Çm s├┤╠ü \(y = f\left( x \right) = \dfrac{2}{3}x + 5\) vãí╠üi \(x \in R\)
Chã░╠üng minh r─â╠Çng ha╠Çm s├┤╠ü ─æ├┤╠Çng bi├¬╠ün tr├¬n \(R\).
-
Bài tập 5 trang 61 SBT Toán 9 Tập 1
Bi├¬╠ëu di├¬╠ân ca╠üc ─æi├¬╠ëm sau ─æ├óy tr├¬n cu╠Çng m├┤╠út h├¬╠ú tru╠úc to╠úa ─æ├┤╠ú. N├┤╠üi theo thã░╠ü tã░╠ú ca╠üc ─æi├¬╠ëm ─æa╠â cho b─â╠Çng ca╠üc ─æoa╠ún th─â╠ëng ─æ├¬╠ë ─æã░ãí╠úc m├┤╠út ─æã░ãí╠Çng g├ó╠üp khu╠üc vãí╠üi ─æi├¬╠ëm ─æ├ó╠Çu la╠Ç ─æi├¬╠ëm A, ─æi├¬╠ëm cu├┤╠üi la╠Ç M.
A(1; 6); B(6; 11); C(14; 12); D(12; 9);
E(15; 8); F(13; 4); G(9; 7); H(12; 1);
I(16; 4); K(20; 1); L(19; 9); M(22; 6).
-
Bài tập 1.1 trang 61 SBT Toán 9 Tập 1
Cho 4 bß║úng ghi c├íc gi├í trß╗ï tã░ãíng ß╗®ng cß╗ºa x v├á y (h.bs.1)
Bảng 1
x 0,5 1 1,5 0,5 2 2,5 y 2,5 3 4,5 3,5 5 6,5 Bảng 2
x -1 -2 1 1,5 1,5 2 y 3 5 3 2 1 5 Bảng 3
x 0 1 1,5 2 2,5 3 y 0 2 3 4 5 6 Bảng 4
x -1 2 -1 3 4 5 y -2 3 2 5,5 6,5 8,5 Trong các bảng trên đây, bảng xác định y là hàm số của x là:
A. Bảng 1
B. Bảng 2
C. Bảng 3
D. Bảng 4.
-
Bài tập 1.2 trang 61 SBT Toán 9 Tập 1
Cho h├ám sß╗æ \(y = f({x}) = 4 - \dfrac{2}{5}x\) vß╗øi \(x \in R\).
Chß╗®ng minh rß║▒ng h├ám sß╗æ ─æ├ú cho nghß╗ïch biß║┐n tr├¬n R.






