Bài tập 4 trang 45 SGK Toán 9 Tập 1

Với bài toán số 4 này, không chỉ việc các em học về đại số, các em còn học và biết thêm các phương pháp vận dụng định lí Pytago để tính ra đại lượng vô tỉ trên mặt phẳng tọa độ.

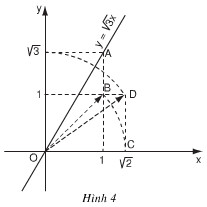
Ta biết rằng đồ thị hàm số \(y = x\sqrt{3}\)  là một đường thẳng đi qua gốc tọa độ. Hơn nữa, khi \(x = 1\) thì \(y = \sqrt{3}\). Do đó điểm \(A(1; \sqrt{3})\) thuộc đồ thị. Vì thế để vẽ đồ thị này, ta phải xác định điểm A trên mặt phẳng tọa độ. Muốn vậy ta phải xác định điểm trên  trục tung biểu diễn số \(\sqrt{3}\). Ta có:

\(\sqrt{3}=\sqrt{1+2}=\sqrt{1^2+(\sqrt{2})^2}\)

Hình vẽ trong SGK thể hiện:

 \(OC = OB =\sqrt{ 2}\)

\(OD=\sqrt{OC^2+CD^2}=\sqrt{2+1}=\sqrt{3}\)

Dùng compa ta xác định được điểm biểu diễn số \(\sqrt{3}\). trên Oy. Từ đó xác định được điểm A

-- Mod Toán 9 HỌC247