Giải bài 25 tr 11 sách BT Toán lớp 9 Tập 2
Giải các hệ phương trình sau bằng phương pháp cộng đại số:
\(a)\left\{ {\matrix{
{2x - 11y = - 7} \cr
{10x + 11y = 31} \cr} } \right.\)
\(b)\left\{ {\matrix{
{4x + 7y = 16} \cr
{4x - 3y = - 24} \cr} } \right.\)
\(c)\left\{ {\matrix{
{0,35x + 4y = - 2,6} \cr
{0,75x - 6y = 9} \cr} } \right.\)
\(d)\left\{ {\matrix{
{\sqrt 2 x + 2\sqrt 3 y = 5} \cr
{4x - 3y = - 24} \cr} } \right.\)
\(e)\left\{ {\matrix{
{10x - 9y = 8} \cr
{15x + 21y = 0,5} \cr} } \right.\)
\(f)\left\{ {\matrix{
{3,3x + 4,2y = 1} \cr
{9x + 14y = 4} \cr} } \right.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Cách giải hệ phương trình bằng phương pháp cộng đại số:
+ Bước 1: Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.
+ Bước 2: Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
+ Bước 3: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.
Lời giải chi tiết
a)
\(\eqalign{
& \left\{ {\matrix{
{2x - 11y = - 7} \cr
{10x + 11y = 31} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{12x = 24} \cr
{2x - 11y = - 7} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = 2} \cr
{2.2 - 11y = - 7} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = 2} \cr
{ - 11y = - 11} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = 2} \cr
{y = 1} \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm (x; y) = (2; 1)
b)
\(\eqalign{
& \left\{ {\matrix{
{4x + 7y = 16} \cr
{4x - 3y = - 24} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{10y = 40} \cr
{4x - 3y = - 24} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = 4} \cr
{4x - 3.4 = - 24} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{y = 4} \cr
{4x = - 12} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = 4} \cr
{x = - 3} \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm (x; y) = (-3; 4)
c)
\(\eqalign{
& \left\{ {\matrix{
{0,35x + 4y = - 2,6} \cr
{0,75x - 6y = 9} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{1,05x + 12y = - 7,8} \cr
{1,5x - 12y = 18} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{2,55x = 10,2} \cr
{0,75x - 6y = 9} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{x = 4} \cr
{0,75.4 - 6y = 9} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = 4} \cr
{ - 6y = 6} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{x = 4} \cr
{y = - 1} \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm (x; y) = (4; -1)
d)
\(\eqalign{
& \left\{ {\matrix{
{\sqrt 2 x + 2\sqrt 3 y = 5} \cr
{3\sqrt 2 x - \sqrt 3 y = {9 \over 2}} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{\sqrt 2 x + 2\sqrt 3 y = 5} \cr
{6\sqrt 2 x - 2\sqrt 3 y = 9} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{7\sqrt 2 x = 14} \cr
{\sqrt 2 x + 2\sqrt 3 y = 5} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{x = {{14} \over {7\sqrt 2 }}} \cr
{\sqrt 2 x + 2\sqrt 3 y = 5} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = \sqrt 2 } \cr
{\sqrt 2 .\sqrt 2 + 2\sqrt 3 y = 5} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{x = \sqrt 2 } \cr
{2\sqrt 3 y = 3} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = \sqrt 2 } \cr
{y = {{\sqrt 3 } \over 2}} \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm (x; y) = \(\left( {\sqrt 2 ;{{\sqrt 3 } \over 2}} \right)\)
e)
\(\eqalign{
& \left\{ {\matrix{
{10x - 9y = 8} \cr
{15x + 21y = 0,5} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{30x - 27y = 24} \cr
{30x + 42y = 1} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{69y = - 23} \cr
{10x - 9y = 8} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{y = - {1 \over 3}} \cr
{10x - 9.\left( { - {1 \over 3}} \right) = 8} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{y = - {1 \over 3}} \cr
{10x = 5} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{y = - {1 \over 3}} \cr
{x = {1 \over 2}} \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm (x; y) = \(\left( {{1 \over 2}; - {1 \over 3}} \right)\)
f)
\(\eqalign{
& \left\{ {\matrix{
{3,3x + 4,2y = 1} \cr
{9x + 14y = 4} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{33x + 42y = 10} \cr
{27x + 42y = 12} \cr
} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{6x = - 2} \cr
{9x + 14y = 4} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{x = - {1 \over 3}} \cr
{9.\left( { - {1 \over 3}} \right) + 14y = 4} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{x = - {1 \over 3}} \cr
{14y = 7} \cr
} } \right. \Leftrightarrow \left\{ {\matrix{
{x = - {1 \over 3}} \cr
{y = {1 \over 2}} \cr} } \right. \cr} \)
Vậy hệ phương trình đã cho có một nghiệm (x; y) = \(\left( { - {1 \over 3};{1 \over 2}} \right)\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 26 trang 19 SGK Toán 9 Tập 2
Bài tập 27 trang 20 SGK Toán 9 Tập 2
Bài tập 26 trang 11 SBT Toán 9 Tập 2
Bài tập 27 trang 11 SBT Toán 9 Tập 2
Bài tập 28 trang 11 SBT Toán 9 Tập 2
Bài tập 29 trang 11 SBT Toán 9 Tập 2
Bài tập 30 trang 11 SBT Toán 9 Tập 2
Bài tập 31 trang 12 SBT Toán 9 Tập 2
Bài tập 32 trang 12 SBT Toán 9 Tập 2
Bài tập 33 trang 12 SBT Toán 9 Tập 2
Bài tập 34 trang 12 SBT Toán 9 Tập 2
Bài tập 4.1 trang 12 SBT Toán 9 Tập 2
-

 Mọi người giúp em vs bài 1 ạ
Mọi người giúp em vs bài 1 ạ Theo dõi (1) 7 Trả lời
Theo dõi (1) 7 Trả lời -


Giải hệ phương trình x-2y=0 và x-y=3
bởi Bích Huyền
 04/04/2020
Bài kiểm tra
04/04/2020
Bài kiểm tra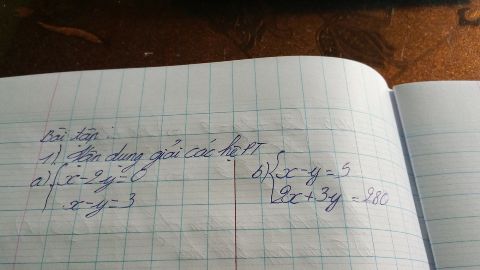 Theo dõi (0) 11 Trả lời
Theo dõi (0) 11 Trả lời -


Giải hệ phương trình căn 2x+2 căn 3 y=5 và 3 căn 2 x - căn 3 y=4,5
bởi Nguyễn Thị Khánh Ngọc
 04/04/2020
04/04/2020
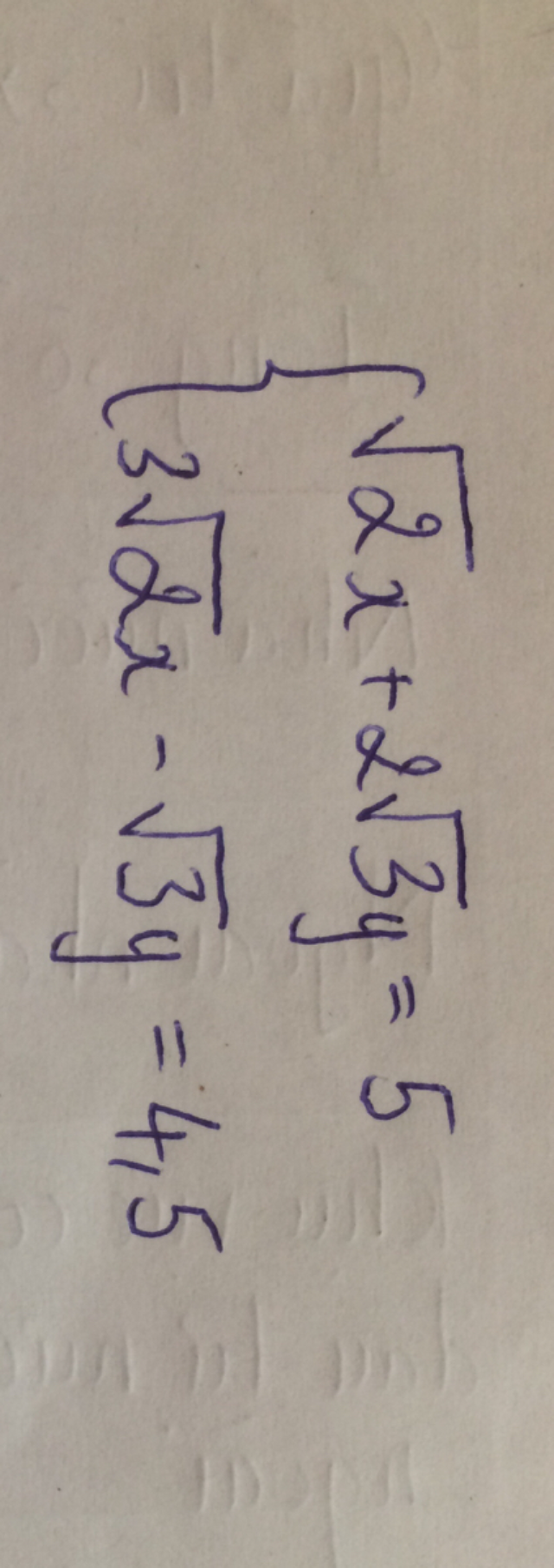 Theo dõi (1) 5 Trả lời
Theo dõi (1) 5 Trả lời -


Giải hệ phương trình x/y=2/3 và x+y-10=0
bởi Thu Hiền
 02/04/2020
02/04/2020
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -
ADMICRO


Giải hệ phương trình x/y=2/3 và x+y-10=0
bởi Thục Hiền
 01/04/2020
Em hỏi cách giải cyar 1g 1i và 1h ạEm cảm ơn
01/04/2020
Em hỏi cách giải cyar 1g 1i và 1h ạEm cảm ơn Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Giải hệ phương trình (x+y)/3+2/3=3 và (4x-y)/6+x/4=1
bởi Thu Hiền
 31/03/2020
31/03/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm x biết căn (2x-1)=3-căn(8x-4)
bởi Đỗ Bình Lan
 31/03/2020
Bài 2 và 3 ạ
31/03/2020
Bài 2 và 3 ạ Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


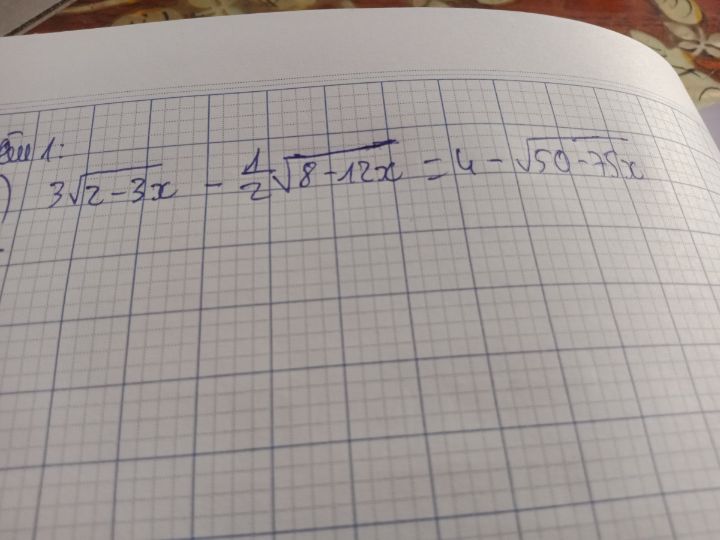 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


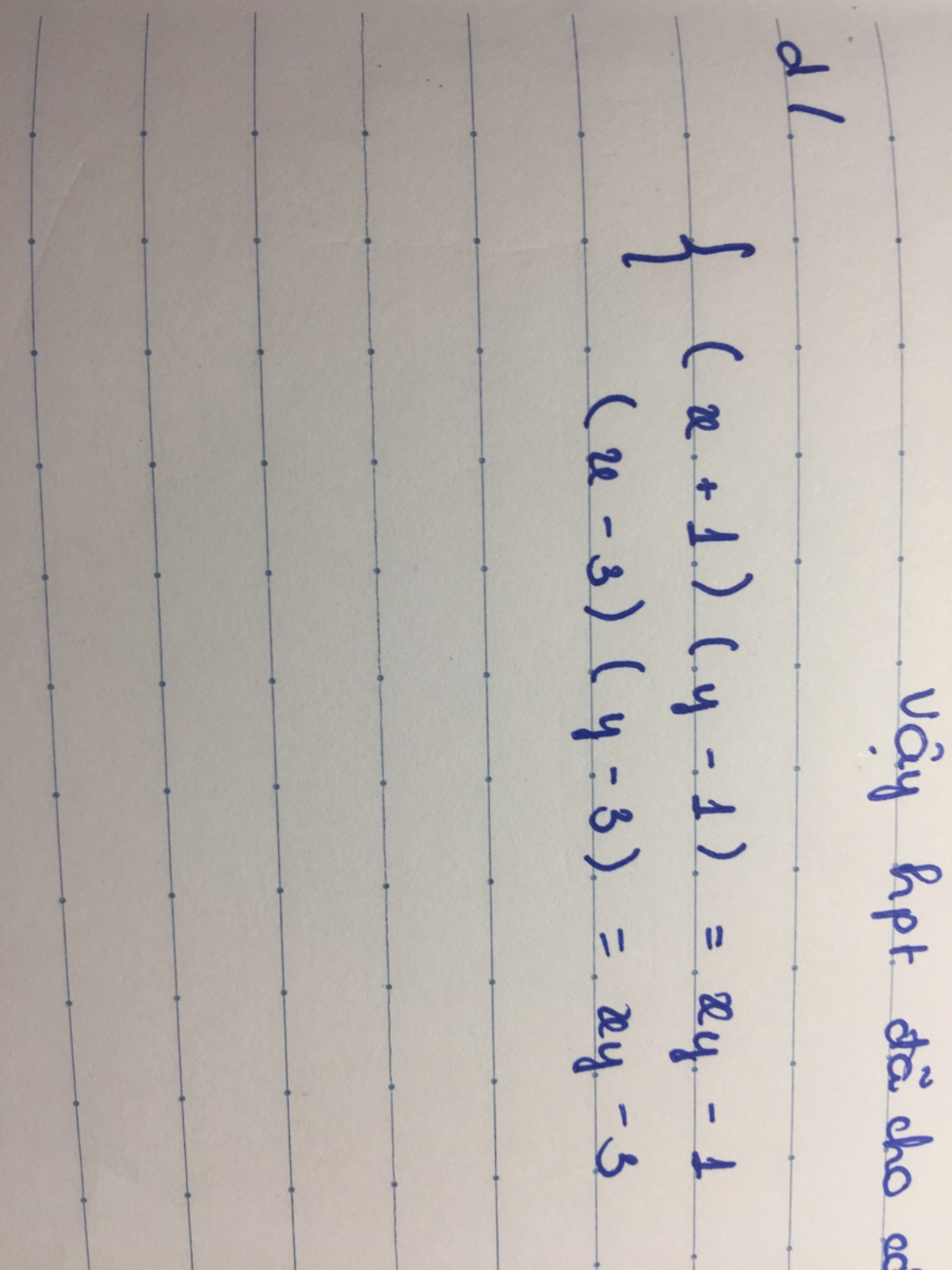 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Giải hệ phương trình 1/x+1/y=5 và 2/x+5/y=7
bởi Vũ Phương Hà Phương
 13/03/2020
13/03/2020
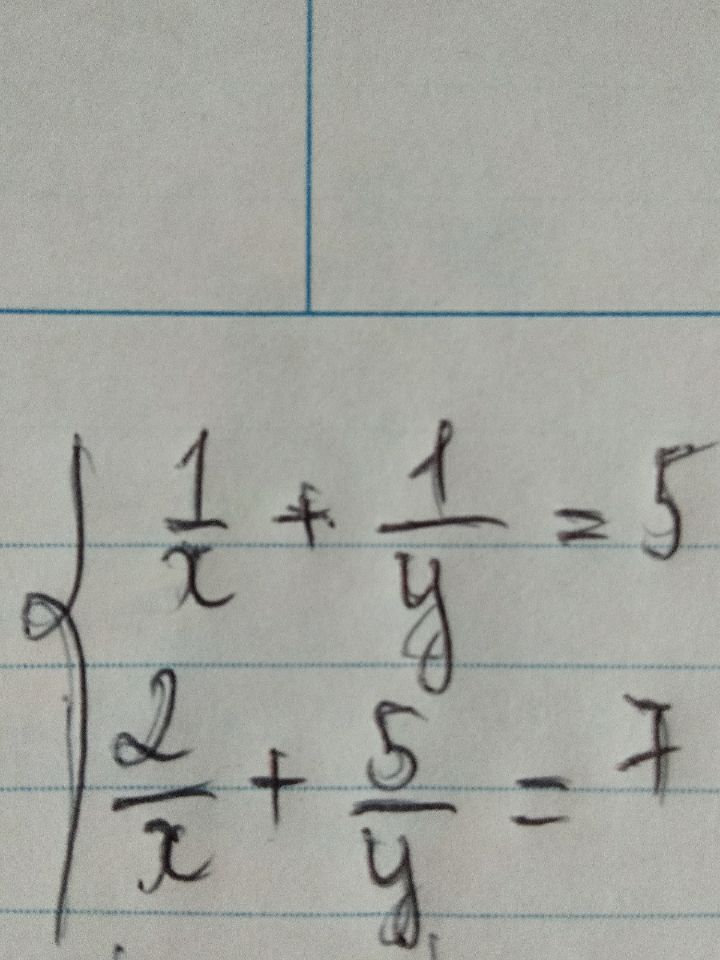 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Giải hệ phương trình (x+1)(y-1)=2 và (x-3)(y+1)=-6
bởi Nguyễn Thanh
 11/03/2020
11/03/2020
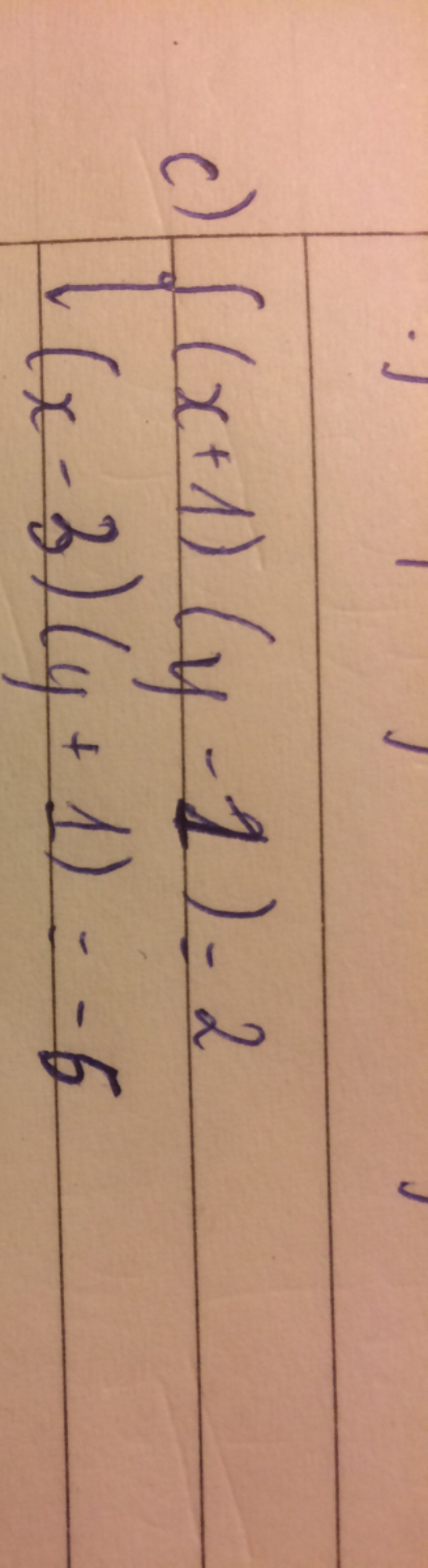 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời





