Toán 7 Cánh diều Bài 5: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh

Ví dụ: Các cặp tam giác nào ở Hình 49 là bằng nhau? Vì sao?

Giải

+ Xét hai tam giác ABC và DEG, ta có:

AB= DE; \(\widehat A = \widehat D\); AC= DG.

Suy ra \(\Delta\)ABC = \(\Delta\)DEG (c.g.c).

+ Xét hai tam giác MNP và ORS, ta có:

MP= QS: \(\widehat P = \widehat S\): NP = RS.

Suy ra \(\Delta\)MNP = \(\Delta\)QRS (c.g.c).

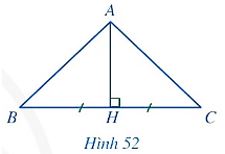
Ví dụ: Hai tam giác AHB và AHC vuông tại H có HB= HC (Hình 52).

Chứng minh:

a) \(\Delta\)AHB = \(\Delta\)AHC;

b) AB = AC.

Giải

a) Xét hai tam giác vuông AHB và AHC, ta có:

AH là cạnh chung; HB = HC (giả thiết).

Suy ra \(\Delta\)AHB = \(\Delta\)AHC (hai cạnh góc vuông).

b) Vì \(\Delta\)AHB = \(\Delta\)AHC nên AB = AC (hai cạnh tương ứng). 

Câu 1: Cho góc nhọn xOy. Hai điểm M, N thuộc tia Ox thỏa mãn OM = 2 cm, ON = 3 cm. Hai điểm P, Q thuộc tia Oy thỏa mãn OP = 2 cm, OQ = 3 cm. Chứng minh MQ = NP.

Hướng dẫn giải

Xét tam giác OMQ và tam giác OPN có: OM = OP (= 2 cm); OQ = ON (= 3 cm); góc O chung.

Vậy \(\Delta OMQ = \Delta OPN\) (c.g.c)

\(\Rightarrow MQ = NP\) ( 2 cạnh tương ứng)

Câu 2: Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thỏa mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP = NP.

Hướng dẫn giải

Xét tam giác MOP và tam giác NOP có: OM = ON, OP chung, \(\widehat {MOP} = \widehat {NOP}\)(vì Oz là tia phân giác).
Vậy \(\Delta MOP = \Delta NOP\)(c.g.c)

\(\Rightarrow MP = NP\) ( 2 cạnh tương ứng)

Qua bài giảng ở trên, giúp các em học sinh:

- Vẽ tam giác khi biết hai cạnh và góc xen giữa. 

- Hiểu được trường hợp bằng nhau c.g.c của hai tam giác.

- Biết chứng minh 2 tam giác bằng nhau theo trường hợp c.g.c.

- Biết sử dụng 2 tam giác bằng nhau để suy ra 2 góc bằng nhau hay hai đoạn thẳng bằng nhau.

Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Toán 7 Cánh diều Chương 7 Bài 5 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 7 Cánh diều Chương 7 Bài 5 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Câu hỏi khởi động trang 84 SGK Toán 7 Cánh diều tập 2 - CD

Hoạt động 1 trang 84 SGK Toán 7 Cánh diều tập 2 - CD

Hoạt động 2 trang 84 SGK Toán 7 Cánh diều tập 2 - CD

Luyện tập 1 trang 85 SGK Toán 7 Cánh diều tập 2 - CD

Luyện tập 2 trang 85 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 1 trang 86 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 2 trang 86 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 3 trang 86 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 4 trang 87 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 31 trang 77 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 32 trang 78 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 33 trang 78 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 34 trang 78 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 35 trang 78 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 36 trang 78 SBT Toán 7 Cánh diều tập 2 - CD

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!