Äáŧ giÚp cÃĄc em háŧc tášp hiáŧu quášĢ mÃīn ToÃĄn 10, Äáŧi ngÅĐ HáŧC247 ÄÃĢ biÊn soᚥn và táŧng háŧĢp náŧi dung bà i TrÆ°áŧng háŧĢp bášąng nhau tháŧĐ ba cáŧ§a tam giÃĄc gÃģc - cᚥnh - gÃģc. Bà i giášĢng gáŧm kiášŋn tháŧĐc cᚧn nháŧ và cÃĄc bà i tášp minh háŧa cÃģ hÆ°áŧng dášŦn giášĢi chi tiášŋt, giÚp cÃĄc em háŧc tášp và cáŧ§ng cáŧ thášt táŧt kiášŋn tháŧĐc. Máŧi cÃĄc em cÃđng tham khášĢo.
TÃģm tášŊt lÃ― thuyášŋt
1.1. TrÆ°áŧng háŧĢp bášąng nhau gÃģc - cᚥnh - gÃģc (g.c.g)
|
Nášŋu máŧt cᚥnh và hai gÃģc liáŧn káŧ cᚥnh ÄÃģ cáŧ§a tam giÃĄc nà y bášąng máŧt cᚥnh và hai gÃģc liáŧn káŧ tÆ°ÆĄng áŧĐng cáŧ§a tam giÃĄc kia thÃŽ hai tam giÃĄc nà y bášąng nhau. |
|---|
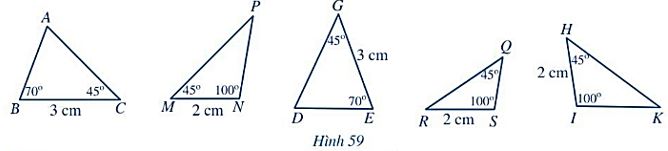
Và dáŧĨ: Quan sÃĄt HÃŽnh 59, cÃĄc cáš·p tam giÃĄc nà o dÆ°áŧi ÄÃĒy là bášąng nhau? VÃŽ sao?
GiášĢi
+ XÃĐt hai tam giÃĄc ABC và DEG, ta cÃģ:
\(\widehat B = \widehat E;BC = EG;\widehat C = \widehat G\).
Suy ra \(\Delta \)ABC = \(\Delta \)DEG (g.c.g).
+ XÃĐt hai tam giÃĄc MNP và HIK, ta cÃģ:
\(\widehat M = \widehat H;MN = HI;\widehat N = \widehat I\).
Suy ra \(\Delta \)MNP = \(\Delta \)HIK (g.c.g).
1.2. Ãp dáŧĨng và o trÆ°áŧng háŧĢp bášąng nhau váŧ cᚥnh gÃģc vuÃīng (hoáš·c cᚥnh huyáŧn) và gÃģc nháŧn cáŧ§a tam giÃĄc vuÃīng
*TrÆ°áŧng háŧĢp bášąng nhau váŧ cᚥnh gÃģc vuÃīng và gÃģc nháŧn cáŧ§a tam giÃĄc vuÃīng
|
Nášŋu máŧt cᚥnh gÃģc vuÃīng và gÃģc nháŧn káŧ cᚥnh ášĨy cáŧ§a tam giÃĄc vuÃīng nà y bášąng máŧt cᚥnh gÃģc vuÃīng và gÃģc nháŧn káŧ cᚥnh ášĨy cáŧ§a tam giÃĄc vuÃīng kia thÃŽ hai tam giÃĄc vuÃīng ÄÃģ bášąng nhau. |
|---|
*TrÆ°áŧng háŧĢp bášąng nhau váŧ cᚥnh huyáŧn và gÃģc nháŧn cáŧ§a tam giÃĄc vuÃīng
|
Nášŋu cᚥnh huyáŧn và máŧt gÃģc nháŧn cáŧ§a tam giÃĄc vuÃīng nà y bášąng cᚥnh huyáŧn và máŧt gÃģc nháŧn cáŧ§a tam giÃĄc vuÃīng kia thÃŽ hai tam giÃĄc vuÃīng ÄÃģ bášąng nhau. |
|---|
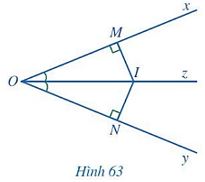
Và dáŧĨ: Cho gÃģc xOy và Oz là tia phÃĒn giÃĄc cáŧ§a gÃģc ÄÃģ. Gáŧi I là máŧt Äiáŧm trÊn tia Oz (I khÃĄc 0). Kášŧ IM vuÃīng gÃģc váŧi Ox (M \(\in\) Ox), IN vuÃīng gÃģc váŧi Oy (N \(\in\) Oy). CháŧĐng máŧnh rášąng IM = IN.
GiášĢi
XÃĐt hai tam giÃĄc vuÃīng IOM và ION, ta cÃģ:
OI là cᚥnh chung;
\(\widehat {IOM} = \widehat {IO{\rm{N}}}\) (vÃŽ Oz là tia phÃĒn giÃĄc cáŧ§a \(\widehat {xOy}\)).
Suy ra \(\Delta \)IOM = \(\Delta \)ION (cᚥnh huyáŧn - gÃģc nháŧn).
Vášy IM = IN (hai cᚥnh tÆ°ÆĄng áŧĐng).
BÃ i tášp minh háŧa
CÃĒu 1: Cho hai tam giÃĄc ABC và AâBâCâ tháŧa mÃĢn: BC = BâCâ = 3 cm, \(\widehat B = \widehat {B'} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A'} = 70^\circ \). Hai tam giÃĄc ABC và AâBâCâ cÃģ bášąng nhau khÃīng? VÃŽ sao?
HÆ°áŧng dášŦn giášĢi
Táŧng ba gÃģc trong máŧt tam giÃĄc bášąng 180°. Vášy trong tam giÃĄc AâBâCâ cÃģ \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
XÃĐt hai tam giÃĄc ABC và AâBâCâ cÃģ:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = BâCâ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vášy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
CÃĒu 2: CÃģ ba trᚥm quan sÃĄt A, B, C trong ÄÃģ trᚥm quan sÃĄt C áŧ giáŧŊa háŧ.
NgÆ°áŧi ta muáŧn Äo khoášĢng cÃĄch táŧŦ A và táŧŦ B Äášŋn C. Do khÃīng tháŧ Äo tráŧąc tiášŋp ÄÆ°áŧĢc cÃĄc khoášĢng cÃĄch trÊn nÊn ngÆ°áŧi ta là m nhÆ° sau (HÃŽnh 55):
- Äo gÃģc BAC ÄÆ°áŧĢc 60o, Äo gÃģc ABC ÄÆ°áŧĢc 45o;
- Kášŧ tia Ax sao cho \(\widehat {BAx} = 60^\circ \), kášŧ tia By sao cho \(\widehat {ABy} = 45^\circ \), xÃĄc Äáŧnh giao Äiáŧm D cáŧ§a hai tia ÄÃģ;
- Äo khoášĢng cÃĄch AD và BD. Ta cÃģ AC = AD và BC = BD.
Tᚥi sao lᚥi cÃģ hai Äášģng tháŧĐc trÊn?
HÆ°áŧng dášŦn giášĢi
XÃĐt hai tam giÃĄc ABC và ABD cÃģ: \(\widehat {CAB} = \widehat {DAB} = 60^\circ ,\widehat {ABC} = \widehat {ABD} = 45^\circ \), AB chung.
Vášy \(\Delta ABC = \Delta ABD\) (g.c.g).
Suy ra AC = AD và BC = BD ( 2 cᚥnh tÆ°ÆĄng áŧĐng)
Luyáŧn tášp ChÆ°ÆĄng 7 BÃ i 6 ToÃĄn 7 CD
Qua bà i giášĢng áŧ trÊn, giÚp cÃĄc em háŧc sinh:
- PhÃĄt biáŧu ÄÆ°áŧĢc trÆ°áŧng háŧĢp bášąng nhau gÃģc - cᚥnh - gÃģc cáŧ§a hai tam giÃĄc
- Biášŋt cÃĄch váš― máŧt tam giÃĄc biášŋt máŧt cᚥnh và hai gÃģc káŧ cᚥnh ÄÃģ.
- Sáŧ dáŧĨng trÆ°áŧng háŧĢp bášąng nhau cáŧ§a hai tam giÃĄc g â c â g Äáŧ cháŧĐng minh hai tam giÃĄc bášąng nhau, táŧŦ ÄÃģ suy ra cÃĄc gÃģc tÆ°ÆĄng áŧĐng bášąng nhau, cÃĄc cᚥnh tÆ°ÆĄng áŧĐng bášąng nhau.
3.1. BÃ i tášp trášŊc nghiáŧm ChÆ°ÆĄng 7 BÃ i 6 ToÃĄn 7 CD
Äáŧ cáŧ§ng cáŧ bà i háŧc xin máŧi cÃĄc em cÃđng là m Bà i kiáŧm tra TrášŊc nghiáŧm ToÃĄn 7 CÃĄnh diáŧu ChÆ°ÆĄng 7 Bà i 6 Äáŧ kiáŧm tra xem mÃŽnh ÄÃĢ nášŊm ÄÆ°áŧĢc náŧi dung bà i háŧc hay chÆ°a.
CÃĒu 4-10: Máŧi cÃĄc em ÄÄng nhášp xem tiášŋp náŧi dung và thi tháŧ Online Äáŧ cáŧ§ng cáŧ kiášŋn tháŧĐc và nášŊm váŧŊng hÆĄn váŧ bà i háŧc nà y nhÃĐ!
3.2. BÃ i tášp SGK ChÆ°ÆĄng 7 BÃ i 6 ToÃĄn 7 CD
BÊn cᚥnh ÄÃģ cÃĄc em cÃģ tháŧ xem phᚧn hÆ°áŧng dášŦn GiášĢi bà i tášp ToÃĄn 7 CÃĄnh diáŧu ChÆ°ÆĄng 7 Bà i 6 Äáŧ giÚp cÃĄc em nášŊm váŧŊng bà i háŧc và cÃĄc phÆ°ÆĄng phÃĄp giášĢi bà i tášp.
CÃĒu háŧi kháŧi Äáŧng trang 88 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
Hoᚥt Äáŧng 1 trang 88 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
Hoᚥt Äáŧng 2 trang 88 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
Luyáŧn tášp 1 trang 89 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
Luyáŧn tášp 2 trang 89 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 1 trang 91 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 2 trang 91 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 3 trang 92 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 4 trang 92 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 5 trang 92 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 6 trang 92 SGK ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 37 trang 81 SBT ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 38 trang 81 SBT ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 39 trang 81 SBT ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 40 trang 81 SBT ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 41 trang 81 SBT ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
GiášĢi bà i 42 trang 81 SBT ToÃĄn 7 CÃĄnh diáŧu tášp 2 - CD
Háŧi ÄÃĄp ChÆ°ÆĄng 7 BÃ i 6 ToÃĄn 7 CD
Trong quÃĄ trÃŽnh háŧc tášp nášŋu cÃģ thášŊc mášŊc hay cᚧn tráŧĢ giÚp gÃŽ thÃŽ cÃĄc em hÃĢy comment áŧ máŧĨc Háŧi ÄÃĄp, Cáŧng Äáŧng ToÃĄn HOC247 sáš― háŧ tráŧĢ cho cÃĄc em máŧt cÃĄch nhanh chÃģng!
ChÚc cÃĄc em háŧc tášp táŧt và luÃīn Äᚥt thà nh tÃch cao trong háŧc tášp!
-- Mod ToÃĄn Háŧc 7 HáŧC247


.JPG)
.JPG)
