Giải bài 2 trang 91 SGK Toán 7 Cánh diều tập 2
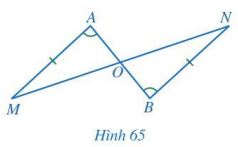
Cho Hình 65 có AM = BN, \(\widehat A = \widehat B\). Chứng minh: OA = OB, OM = ON.
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
Chứng minh tam giác AOM bằng tam giác BON.
Lời giải chi tiết
Ta có: \(\widehat A = \widehat B\)
Mà 2 góc này ở vị trí so le trong nên AM // BN
\(\Rightarrow \widehat M = \widehat N\)(2 góc so le trong).
Xét hai tam giác AOM và BON có: \(\widehat A = \widehat B\), AM = BN, \(\widehat M = \widehat N\).
Vậy \(\Delta AOM = \Delta BON\) (g.c.g)
Do đó OA = OB, OM = ON. (2 cạnh tương ứng).
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Luyện tập 2 trang 89 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 1 trang 91 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 3 trang 92 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 4 trang 92 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 5 trang 92 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 6 trang 92 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 37 trang 81 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 38 trang 81 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 39 trang 81 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 40 trang 81 SBT Toán 7 Cánh diều tập 2 - CD
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.