Nội dung bài giảng Tính chất ba đường cao của tam giác môn Toán lớp 7 chương trình Cánh Diều được HOC247 biên soạn và tổng hợp giới thiệu đến các em học sinh, giúp các em dễ dàng nắm được nội dung chính của bài. Để đi sâu vào tìm hiểu và nghiên cứu nội dung vài học, mời các em cùng tham khảo nội dung chi tiết trong bài giảng sau đây.
Tóm tắt lý thuyết
1.1. Đường cao của tam giác
|
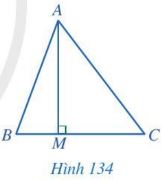
Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là một đường cao của tam giác đó. |
|---|
Trong Hình 134, đoạn thẳng AM là một đường cao của tam giác ABC. Đôi khi, ta cũng gọi đường thẳng AM là một đường cao của tam giác ABC.
Ví dụ: Trong ba đoạn thẳng AH, BK, DN, đoạn thẳng nào là đường cao của tam giác ABC (Hình 135)?
Giải
+ Đoạn thẳng AH không là đường cao của tam giác ABC vì A là đỉnh của tam giác ABC mà AH không vuông góc với BC.
+ Đoạn thẳng BK là đường cao của tam giác ABC vì B là đỉnh của tam giác ABC và BK vuông góc với AC.
+ Đoạn thẳng DN không là đường cao của tam giác ABC vì cả D và N không là đỉnh của tam giác ABC.
Nhận xét
+ Mỗi tam giác có ba đường cao;
+ Đường cao của tam giác có thể nằm trong, trên cạnh, hoặc nằm ngoài tam giác.
1.2. Tính chất ba đường cao của tam giác
Định lí:
|
Trong một tam giác, ba đường cao cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác. |
|---|
Nhận xét: Để xác định trực tâm của một tam giác, ta chỉ cần vẽ hai đường cao bất kì và xác định giao điểm của hai đường đó.
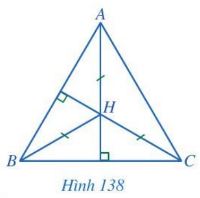
Ví dụ: Cho tam giác ABC có trực tâm H thoả mãn HA = HB = HC (Hình 138).
Chứng minh tam giác ABC đều.
Giải
Vì HB = HC nên H thuộc đường trung trực của cạnh BC.
Vì H là trực tâm tam giác AC nên AH \( \bot \) BC.
Đường thẳng AH và đường trung trực của cạnh BC cùng đi qua H và vuông góc với BC nên chúng trùng nhau.
Suy ra AH là đường trung trực của BC. Do đó AB = AC. Chứng minh tương tự, ta có BC = CA.
Suy ra AB = BC = CA. Vậy tam giác ABC đều.
Bài tập minh họa
Câu 1: Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C.
Hướng dẫn giải
Đường cao đi qua B là AB.
Đường cao đi qua C là AC.
Câu 2: Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.
Hướng dẫn giải
Tam giác ABC đều nên AB = AC = BC.
G là trọng tâm tam giác ABC nên AD, BE, CF là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD.
Xét tam giác ADB và tam giác ADC có:
AB = AC (tam giác ABC đều);
AD chung
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.c.c) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà ba điểm B, D, C thẳng hàng nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \)hay \(AD \bot BC\). (1)
Tương tự ta có:
\(\widehat {AEB} = \widehat {CEB} = 90^\circ \) hay\(BE \bot AC\). (2)
\(\widehat {AFC} = \widehat {BFC} = 90^\circ \) hay\(CF \bot AB\). (3)
Từ (1), (2), (3) suy ra G là giao điểm của ba đường cao AD, BE, CF.
Vậy G cũng là trực tâm của tam giác ABC.
Luyện tập Chương 7 Bài 13 Toán 7 CD
Qua bài giảng ở trên, giúp các em học sinh:
- Biết khái niệm đường cao của tam giác và mỗi tam giác có ba đường cao.
- Luyện cách dùng êke để vẽ đường cao của tam giác.
- Qua vẽ hình nhận biết ba đường cao của tam giác luôn đi qua một điểm. Từ đó vận dụng định lí về tính chất đồng quy của ba đường cao của tam giác để giải bài tập.
3.1. Bài tập trắc nghiệm Chương 7 Bài 13 Toán 7 CD
Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Toán 7 Cánh diều Chương 7 Bài 13 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK Chương 7 Bài 13 Toán 7 CD
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 7 Cánh diều Chương 7 Bài 13 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Câu hỏi khởi động trang 116 SGK Toán 7 Cánh diều tập 2 - CD
Hoạt động 1 trang 116 SGK Toán 7 Cánh diều tập 2 - CD
Luyện tập 1 trang 117 SGK Toán 7 Cánh diều tập 2 - CD
Hoạt động 2 trang 117 SGK Toán 7 Cánh diều tập 2 - CD
Luyện tập 2 trang 117 SGK Toán 7 Cánh diều tập 2 - CD
Luyện tập 3 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 1 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 2 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 3 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 4 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 5 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 6 trang 118 SGK Toán 7 Cánh diều tập 2 - CD
Giải bài 92 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 93 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 94 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 95 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 96 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 97 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Giải bài 98 trang 97 SBT Toán 7 Cánh diều tập 2 - CD
Hỏi đáp Chương 7 Bài 13 Toán 7 CD
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 7 HỌC247


.JPG)
.JPG)
