Toán 7 Cánh diều Bài 10: Tính chất ba đường trung tuyến của tam giác

+ Đôi khi, đường thẳng AM cũng được gọi là đường trung tuyến của tam giác ABC.

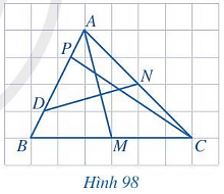
Ví dụ: Trong ba đoạn thẳng AM, DN, CP (Hình 98), đoạn thẳng nào là đường trung tuyến của tam giác ABC?

Giải

+ Đoạn thẳng AM là đường trung tuyến của tam giác ABC vì A là đỉnh của tam giác ABC và M là trung điểm của cạnh BC.

+ Đoạn thẳng DN không là đường trung tuyến của tam giác ABC vì cả D và N không là đỉnh của tam giác ABC.

+ Đoạn thẳng CP không là đường trung tuyến của tam giác ABC vì C là đỉnh của tam giác ABC mà P không là trung điểm của cạnh AB.

Nhận xét: Mỗi tam giác có ba đường trung tuyến

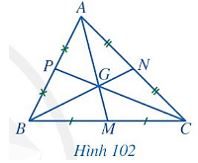
Chú ý: Trong tam giác ABC, ba đường trung tuyến AA, BN, CP cùng đi qua điểm G, ta còn nói chúng đồng quy tại điểm G (Hình 102). Do đó, để xác định trọng tâm của một tam giác, ta chỉ cần vẽ hai đường trung tuyến bất kì và xác định giao điểm của hai đường đó.

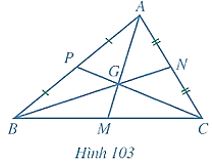
Ví dụ: Cho tam giác ABC có hai đường trung tuyến 8N và CP cắt nhau tại G. Đường thẳng AG cắt BC tại ẤM (Hình 103).

Chứng minh rằng AM là trung điểm của cạnh BC.

Giải

Hai đường trung tuyến BN và CP cắt nhau tại G nên G là trọng tâm của tam giác ABC. Vì G \(\in\) AM nên AM là đường trung tuyến của tam giác ABC. Vậy M là trung điểm của cạnh BC. 

Câu 1: Trong Hình sau, đoạn thẳng HK là đường trung tuyến của những tam giác nào?

Hướng dẫn giải

Đoạn thẳng HK là đường trung tuyến của tam giác: KAC (đỉnh K và trung điểm H của cạnh AC) và HBC (đỉnh H và trung điểm K của cạnh BC).

Câu 2: Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.

Hướng dẫn giải

Ta có G là giao điểm của hai đường trung tuyến QM và RK.

Mà I là trung điểm của QR nên PI cũng là đường trung tuyến trong tam giác PQR.

Vậy PI giao với QM và RK tại G

Do đó, G thuộc PI hay ba điểm P, G, I thẳng hàng.

Qua bài giảng ở trên, giúp các em học sinh:

- Nắm được khái niệm đường trung tuyến (xuất phát từ một đỉnh hoặc ứng với 1 cạnh) của tam giác và nhận thấy mỗi tam giác có 3 đường trung tuyến.

 - Vẽ các đường trung tuyến của một tam giác.

 - Biết sử dụng tính chất ba đường trung tuyến của một tam giác để giải một số bài tập đơn giản.

Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Toán 7 Cánh diều Chương 7 Bài 10 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 7 Cánh diều Chương 7 Bài 10 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Câu hỏi khởi động trang 104 SGK Toán 7 Cánh diều tập 2 - CD

Hoạt động 1 trang 104 SGK Toán 7 Cánh diều tập 2 - CD

Luyện tập 1 trang 105 SGK Toán 7 Cánh diều tập 2 - CD

Hoạt động 2 trang 105 SGK Toán 7 Cánh diều tập 2 - CD

Luyện tập 2 trang 105 SGK Toán 7 Cánh diều tập 2 - CD

Hoạt động 3 trang 106 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 1 trang 107 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 2 trang 107 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 3 trang 107 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 4 trang 107 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 5 trang 107 SGK Toán 7 Cánh diều tập 2 - CD

Giải bài 70 trang 89 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 71 trang 89 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 72 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 73 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 74 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 75 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 76 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 77 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Giải bài 78 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!