Giải bài 74 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Phương pháp giải

Sử dụng tính chất ba đường trung tuyến của tam giác để chứng minh: \(BI = IK = EK = \frac{1}{3}BE\) 

Lời giải chi tiết

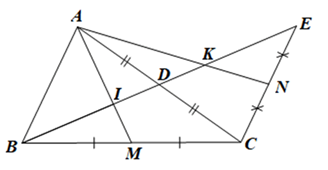
Xét tam giác ABC có BD và AM là các đường trung tuyến, BD cắt AM tại I.

Suy ra I là trọng tâm của tam giác ABC.

Nên \(BI = \frac{2}{3}B{\rm{D}}\)(1)

Xét tam giác AEC có ED và AN là các đường trung tuyến, ED cắt AN tại K.

Suy ra K là trọng tâm của tam giác AEC.

Nên \(EK = \frac{2}{3}E{\rm{D}}\)(2)

Mặt khác BD = DE, DB + DE = BE

Nên \(B{\rm{D}} = DE = \frac{1}{3}BE\)(3)

Từ (1), (2) và (3) ta có:

\(BI = EK = \frac{2}{3}B{\rm{D}} = \frac{2}{3}.\frac{1}{2}BE = \frac{1}{3}BE\).

Ta lại có: BI + IK + KE = BE.

Suy ra \(\frac{1}{3}BE + IK + \frac{1}{3}BE = BE\)

Suy ra \(IK = \frac{1}{3}BE\)

Do đó BI = IK = EK (cùng bằng \(\frac{1}{3}BE\)).

Vậy BI = IK = EK.

-- Mod Toán 7 HỌC247