Giải bài 75 trang 90 SBT Toán 7 Cánh diều tập 2 - CD

Phương pháp giải

- Chứng minh hai tam giác AMD và AMC cân tại M.

- Tổng ba góc của một tam giác bằng \({180^o}\).

Từ đó chứng minh \(\widehat {BAC} = {90^o}\)

Lời giải chi tiết

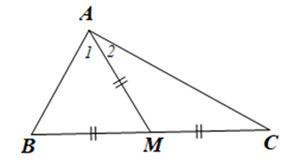
Ta có: \(AM = \frac{1}{2}BC\), BM = MC nên AM = BM = MC.

Suy ra hai tam giác AMB và AMC cân tại M.

Do đó \(\hat B = {\hat A_1},\hat C = {\hat A_2}\)

Xét DABC có \(\hat B + \hat C + \widehat {BAC} = 180^\circ \) (tổng ba góc của một tam giác)

Suy ra \({\hat A_1} + {\hat A_2} + \widehat {BAC} = 180^\circ \) hay \(\widehat {BAC} + \widehat {BAC} = 180^\circ \)

Nên 2ˆBAC=180°2BAC^=180°

Do đó \(\widehat {BAC} = \frac{{180^\circ }}{2} = 90^\circ \)

Vậy \(\widehat {BAC} = 90^\circ \)

-- Mod Toán 7 HỌC247