Giải bài 5 tr 26 sách GK Toán Hình lớp 12
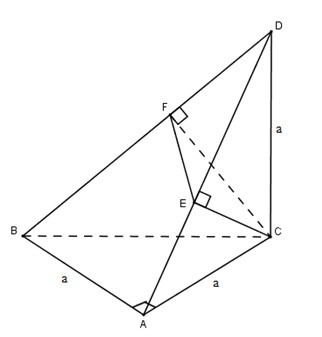
Cho tam giác ABC vuông cân ở A và AB = a. Trên đường thẳng qua C và vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua C vuông góc với SD, cắt BD tại F và cắt AD tại E. Tình thể tích khối tứ diện CDEF theo a.
Hướng dẫn giải chi tiết bài 5
\(\left. \begin{array}{l}
BA \bot CD\\
BA \bot CA
\end{array} \right\} \Rightarrow BA \bot \left( {ADC} \right) \Rightarrow BA \bot CE\)
Mặt khác BD ⊥ (CEF) ⇒ BD ⊥ CE.
Từ đó suy ra
CE ⊥ (ABD) ⇒ CE ⊥ EF, CE ⊥ AD.
Vì tam giác ACD vuông cân, AC = CD = a nên \(CE = \frac{{AD}}{2} = \frac{{a\sqrt 2 }}{2}\)
Ta có:
\(BC = a\sqrt 2 .BD = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \)
Để ý rằng \(CF.CD = DC.BC\)
Nên \(CF = \frac{{{a^2}\sqrt 2 }}{{a\sqrt 3 }} = a\sqrt {\frac{2}{3}} \)
Từ đó suy ra
\(\begin{array}{l}
EF = \sqrt {C{F^2} - C{E^2}} \\
= \sqrt {\frac{2}{3}{a^2} - \frac{{{a^2}}}{2}} = \frac{{\sqrt 6 }}{6}
\end{array}\).
\(\begin{array}{l}
DF = \sqrt {D{C^2} - C{F^2}} \\
= \sqrt {{a^2} - \frac{{2{a^2}}}{3}} = \frac{{\sqrt 3 }}{3}
\end{array}\).
Từ đó suy ra :
\(\begin{array}{l}
{S_{\Delta CEF}} = \frac{1}{2}FE.FC = \frac{1}{2}.\frac{{a\sqrt 6 }}{6}.\frac{{a\sqrt 2 }}{2}\\
= \frac{{{a^2}\sqrt 3 }}{{12}}
\end{array}\)
Vậy \({V_{D.CEF}} = \frac{1}{3}{S_{\Delta CEF}}.DF\)
\( = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{{12}}.\frac{{a\sqrt 3 }}{3} = \frac{{{a^3}}}{{36}}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3 trang 25 SGK Hình học 12
Bài tập 4 trang 25 SGK Hình học 12
Bài tập 6 trang 26 SGK Hình học 12
Bài tập 1.10 trang 18 SBT Hình học 12
Bài tập 1.11 trang 18 SBT Hình học 12
Bài tập 1.12 trang 18 BT Hình học 12
Bài tập 1.13 trang 18 SBT Hình học 12
Bài tập 1.14 trang 18 SBT Hình học 12
Bài tập 1.15 trang 19 SBT Hình học 12
Bài tập 1.16 trang 19 SBT Hình học 12
Bài tập 1.17 trang 19 SBT Hình học 12
Bài tập 15 trang 28 SGK Hình học 12 NC
Bài tập 16 trang 28 SGK Hình học 12 NC
Bài tập 17 trang 28 SGK Hình học 12 NC
Bài tập 18 trang 28 SGK Hình học 12 NC
Bài tập 19 trang 28 SGK Hình học 12 NC
Bài tập 20 trang 28 SGK Hình học 12 NC
Bài tập 21 trang 28 SGK Hình học 12 NC
Bài tập 22 trang 28 SGK Hình học 12 NC
Bài tập 23 trang 29 SGK Hình học 12 NC
-


Tính thể tích của khối chóp S.ABC có đáy là tam giác vuông cân tại B, AB = a
bởi Huyền Trang
 22/12/2019
Giải câu 23
22/12/2019
Giải câu 23 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tính thể tích của khối chóp A'.BCD biết diện tích các mặt ABCD, ABB'A', ADD'A' lần lượt là 4, 9, 16
bởi trângnantoan
 19/12/2019
JsjshdhdhdhdhTheo dõi (1) 2 Trả lời
19/12/2019
JsjshdhdhdhdhTheo dõi (1) 2 Trả lời -


Tính thể tích V của khối cầu tương ứng biết mặt cầu có diện tích bằng 100pi
bởi vầy thị ơn
 17/12/2019
17/12/2019
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -
ADMICRO


Tính thể tích khối lặng trụ ABC.A'B'C' có đáy là tam giác đều cạnh 3a, A'A=A'B=A'C=4a
bởi Nguyễn Thanh Hoài
 16/12/2019
Giải bài tậpTheo dõi (0) 0 Trả lời
16/12/2019
Giải bài tậpTheo dõi (0) 0 Trả lời -


Tính diện tích S của mặt cầu biết O là tâm của mặt cầu đi qua 8 đỉnh của hình lập phương
bởi Nguyên Diệu Linh
 16/12/2019
Giúp mk với
16/12/2019
Giúp mk với Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính thể tích khối chóp S.ABC có đáy ABC là tam giác vuông tại B biết AB =a, AC=2a
bởi Trà Lăng Thu
 16/12/2019
16/12/2019
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -

 Tính thể tích lăng trụ. Mong mọi người giải chi tiết giúp em ạ
Tính thể tích lăng trụ. Mong mọi người giải chi tiết giúp em ạ Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -

 Thể tích của đa diện đềuTheo dõi (0) 1 Trả lời
Thể tích của đa diện đềuTheo dõi (0) 1 Trả lời -


Tính thể tích khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a và SAB là tam giác cân
bởi Phạm Thị Bích Ngọc
 15/12/2019
15/12/2019
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Thể tích của khối chóp có giá trị lớn nhất là bao nhiêu biết khối chóp có đáy là hình bình hành có 1 cạnh bằng 4a?
bởi Hạ Bùi
 15/12/2019
Câu 21
15/12/2019
Câu 21 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính khoảng cách từ D đến mp(SBC) biết hình chóp S.ABCD có đáy là hình chữ nhật tâm I
bởi Hoàng Minh Vượng
 14/12/2019
Giúp ạ
14/12/2019
Giúp ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Làm câubttong chụp
Làm câubttong chụp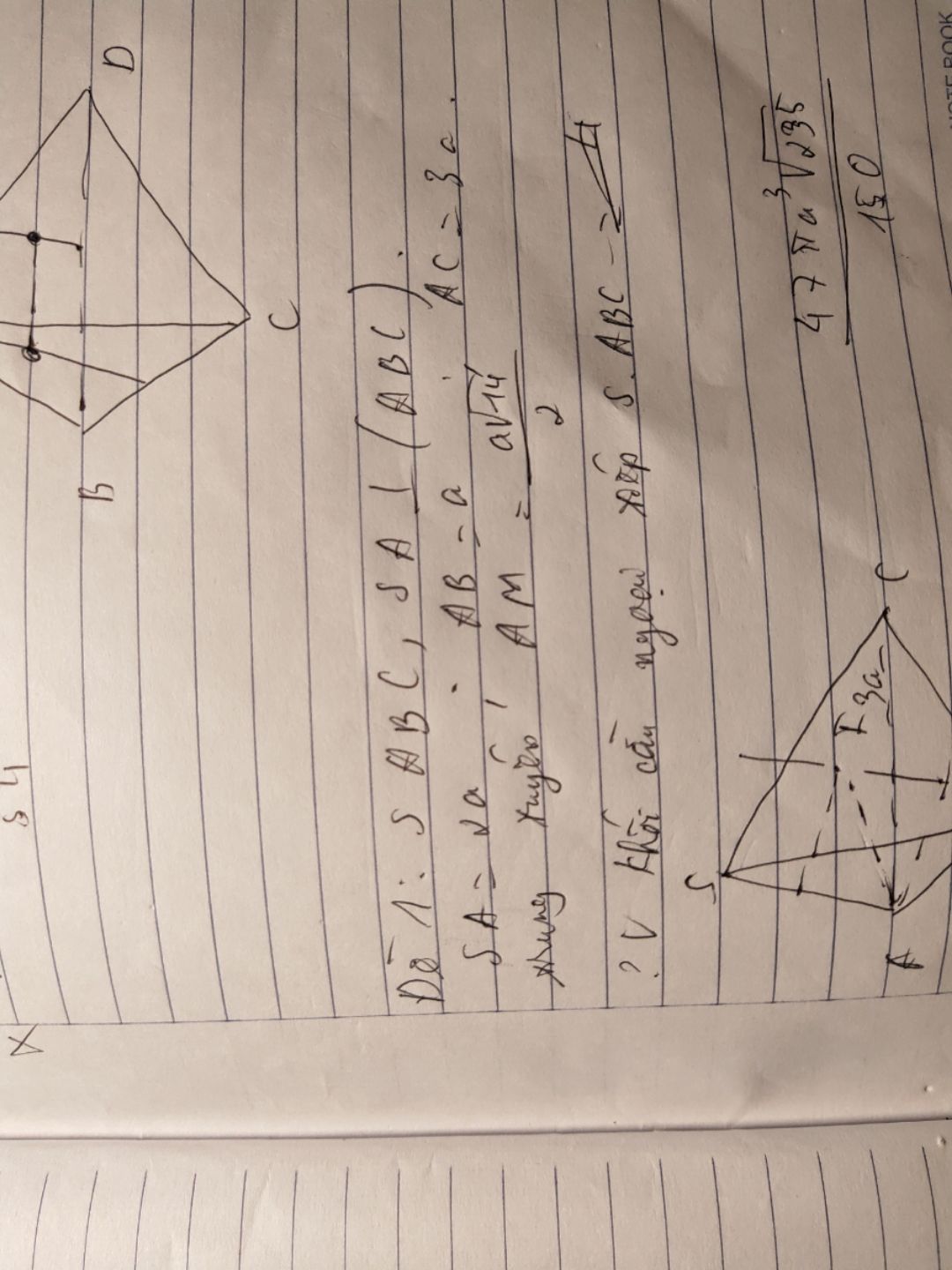 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính thể tích hình cầu ngoại tiếp hình chóp S.ABC có đáy tam giác vuông cân tại A
bởi Nguyễn Thị Thúy Kiều
 13/12/2019
cho hình chóp sabc đáy abc là tam giác vuông cân tại a có ab = a. mặt bên sbc vuông góc với đáy , các mặt bên sab , sac cùng tạo với đáy góc 60°. tính thể tích hình cầu ngoại tiếp hình chóp trênTheo dõi (0) 0 Trả lời
13/12/2019
cho hình chóp sabc đáy abc là tam giác vuông cân tại a có ab = a. mặt bên sbc vuông góc với đáy , các mặt bên sab , sac cùng tạo với đáy góc 60°. tính thể tích hình cầu ngoại tiếp hình chóp trênTheo dõi (0) 0 Trả lời -


Tính thể tích của khối cầu ngoại tiếp hình chóp CMNP biết hình chóp S.ABCD có đáy là hình vuông cạnh 2a căn 2
bởi Quân Minh
 12/12/2019
Giải cứu mình với
12/12/2019
Giải cứu mình với Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh A B = a , A D = a √ 2 , S A ⊥ ( A B C D ) góc giữa SC và đáy bằng 60 độ. Tính thể tích hình chóp S.ABCD.Theo dõi (0) 1 Trả lời
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh A B = a , A D = a √ 2 , S A ⊥ ( A B C D ) góc giữa SC và đáy bằng 60 độ. Tính thể tích hình chóp S.ABCD.Theo dõi (0) 1 Trả lời -


Xác đinh tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD có đáy ABCD là hình chữ nhật
bởi Thảo Mmèo
 11/12/2019
11/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính thể tích v1 của khối lăng trụ abc.a'b'c' biết khối lập phương abcd.a'b'c'd' có thể tích v=1
bởi Thư Võ Minh
 11/12/2019
Cho khối lập phương abcd.a'b'c'd' có thể tích v=1 tính thể tích v1 của khối lăng trụ abc.a'b'c'Theo dõi (0) 2 Trả lời
11/12/2019
Cho khối lập phương abcd.a'b'c'd' có thể tích v=1 tính thể tích v1 của khối lăng trụ abc.a'b'c'Theo dõi (0) 2 Trả lời -

 Giúp em câu 15 với mọi người ơi
Giúp em câu 15 với mọi người ơi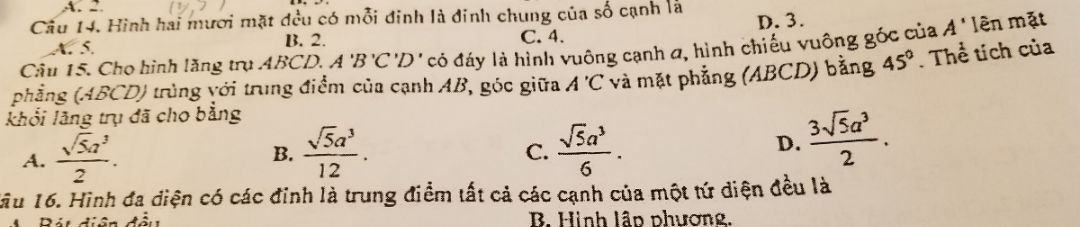 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Tính độ dài đường cao của tứ diện đều có cạnh bằng a
bởi Lê Thị Lợi
 09/12/2019
09/12/2019
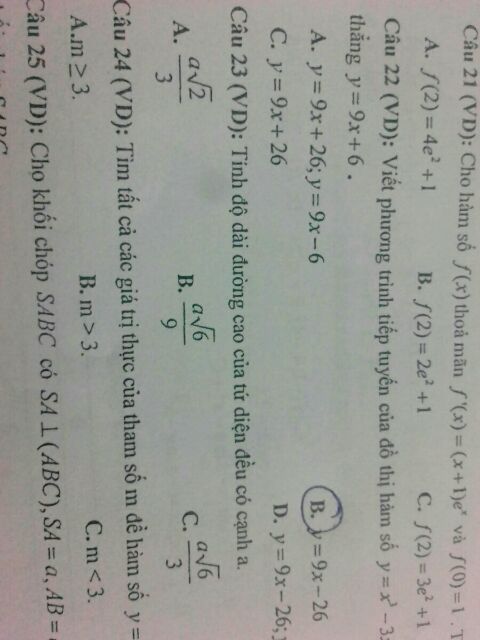 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tính thể tích tứ diện đều cạnh a
bởi Nguyễn Thành Phát
 08/12/2019
08/12/2019
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Cho lăng trụ abc.a'b'c' có đáy abc là tam giác vuông cân tại b và ac = 2a biết (a'bc) hợp với đáy abc 1 góc 45°. Thể tích lăng trụ là :Theo dõi (0) 0 Trả lời
Cho lăng trụ abc.a'b'c' có đáy abc là tam giác vuông cân tại b và ac = 2a biết (a'bc) hợp với đáy abc 1 góc 45°. Thể tích lăng trụ là :Theo dõi (0) 0 Trả lời



