Giải bài 1.10 tr 18 SBT Hình học 12
Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a, các cạnh bên tạo với đáy một góc 600. Hãy tính thể tích của khối chóp đó.
Hướng dẫn giải chi tiết
.png)
Kẻ \(SH \bot (ABC)\). Đường thẳng AH cắt BC tại I.
Do S.ABC là hình chóp tam giác đều nên H là trọng tâm của \({\rm{\Delta }}ABC\).
Do đó:
\(AI = \frac{{\sqrt 3 }}{2}a,AH = \frac{2}{3}.\frac{{\sqrt 3 }}{2}a = \frac{{\sqrt 3 }}{3}a,\)
\(\widehat {SAH} = {60^0}\)
\(SH = AH.\tan {60^0} = \frac{{\sqrt 3 }}{3}a.\sqrt 3 = a\)
Thể tích khối chóp S.ABC là:
\(V = \frac{1}{3}.\frac{1}{2}.\frac{{\sqrt 3 }}{2}a.a.a = \frac{{\sqrt 3 }}{{12}}{a^3}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 5 trang 26 SGK Hình học 12
Bài tập 6 trang 26 SGK Hình học 12
Bài tập 1.11 trang 18 SBT Hình học 12
Bài tập 1.12 trang 18 BT Hình học 12
Bài tập 1.13 trang 18 SBT Hình học 12
Bài tập 1.14 trang 18 SBT Hình học 12
Bài tập 1.15 trang 19 SBT Hình học 12
Bài tập 1.16 trang 19 SBT Hình học 12
Bài tập 1.17 trang 19 SBT Hình học 12
Bài tập 15 trang 28 SGK Hình học 12 NC
Bài tập 16 trang 28 SGK Hình học 12 NC
Bài tập 17 trang 28 SGK Hình học 12 NC
Bài tập 18 trang 28 SGK Hình học 12 NC
Bài tập 19 trang 28 SGK Hình học 12 NC
Bài tập 20 trang 28 SGK Hình học 12 NC
Bài tập 21 trang 28 SGK Hình học 12 NC
Bài tập 22 trang 28 SGK Hình học 12 NC
Bài tập 23 trang 29 SGK Hình học 12 NC
-
Tính thể tích khối chóp S.ABC có đáy là tam giác đều cạnh a góc SAB= góc SCB =90°
bởi Ngọc Hân Nguyễn
28/09/2019
Cho hình chóp S. ABC có đáy là tam giác đều cạnh a góc SAB= góc SCB =90°. Gọi M là trung điểm SA. Khoảng cách từ A đến mặt phẳng ( MBC ) = 6a/7. Tính thể tích khối chóp S. ABCTheo dõi (4) 1 Trả lời -
Tính V của khối chóp S.ABC có đáy là tam giác vuông cân tại B, AB=BC=a
bởi Hương Nguyễn Mai
27/09/2019
Cho hình chóp SABC, đáy là tam giác vuông cân tại B. AB=BC=a. SA vuông góc (ABC). SB hợp với góc (SAB) 1 góc 30°. Tính VTheo dõi (0) 5 Trả lời -
Tính thể tích V của khối chóp S.ABC biết khoảng cách từ A đến mp(MBC) bằng 6a/7
bởi Nguyễn Huyền Tranng
27/09/2019
Tính khoảng cách
Theo dõi (0) 4 Trả lời -
Tính V của khối chóp đều S.ABC có cạnh đáy bằng 2a, góc giữa SA và mp(ABC) bằng 30 độ
bởi vothugiang
25/09/2019
Theo dõi (1) 3 Trả lời -
ADMICRO
Cho tam giác ABC đáy là tam giác đều cạnh a góc sab và góc scb = 900. M là trung điểm cạnh SA.Khoảng cách từ A đến (MBC) là 6a/7.Tính VS.ABC
Theo dõi (0) 9 Trả lời -
Tính thể tích khối chóp SABC theo a biết hình chiếu vuông góc của đỉnh S lên (ABC) là trung diểm H của BC
bởi Phương Thơ
07/08/2019
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B với AB=a, BC=2a. Hình chiếu vuông góc của đỉnh S lên (ABC) là trung diểm H của BC. Góc giữa SA và mặt đáy (ABC) bằng 60 độ. Tính thể tích khối chóp SABC theo a.
Theo dõi (1) 6 Trả lời -
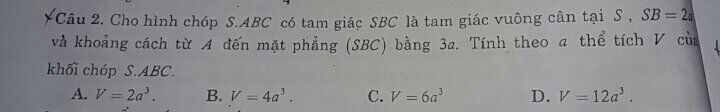Theo dõi (1) 8 Trả lời -
Tính khoảng cách từ B đến (SAC) biết tam giác SBC đều và nằm trong mặt phẳng vuông với đáy
bởi Uyên Trần Thị Tố
04/06/2019
Mọi người giúp mình giải bài tập này với : —- Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A . AB = 1 , AC = căn 3 . Tam giác SBC đều và nằm trong mặt phẳng vuông với đáy . Tính khoảng cách từ B đến mặt phẳng ( SAC ) ———Toán 12 ạhhhh———-Theo dõi (2) 4 Trả lời -
cho tứ diện ABCD có đáy BCD là tam giác đều cạnh a, tâm G. đường thẳng d qua G và vuông góc với (BCD), A chạy trên đường thẳng d sao cho mặt cầu ngoại tiếp ABCD có thể tích nhỏ nhất. Khi đó thể tích của khối ABCD là?
Theo dõi (0) 1 Trả lời -
Tính thể tích hình hộp mà tổng a+b+c lớn nhất nội tiếp trong hình cầu bán kính R
bởi Nguyễn Ngọc Phương Thanh
14/12/2018
Xét tất cả các hình hộp có ba kích thước a,b,c nội tiếp trong hình cầu bán kính R. Hình hộp mà tổng a+b+c lớn nhất có thể tích là
Theo dõi (0) 5 Trả lời -
Cho hình chóp đều SABCD có AB=a,SA=2a. Mặt phẳng (P) qua A,C đồng thời vuông góc với mặt phẳng (SCD). Mặt phẳng (P) cắt SD tại M thì tỉ số VSACM/VSABCD
A.
B.
C.
D.
Theo dõi (0) 8 Trả lời -
Tính tỉ số thể tích của tứ diệm MNCP và ABCD biết trung điểm các cạnh AC, BD, CD là M,N,P
bởi Nguyễn Ngọc Phương Thanh
09/12/2018
Cho tứ diện ABCD có trung điểm cấc cạnh AC,BD,CD lần lượt tại M,N,P. Tỉ số thể tích của tứ diệm MNCP và ABCD là
A.
B.
C.
D.
Theo dõi (0) 5 Trả lời -
Tính thể tích khối chóp S.ABCD biết góc giữa mặt phẳng (SBD) và (ABCD) = 30 độ
bởi đỗ thị hà
09/12/2018
cho hình chóp SABCD đáy là hình chữ hật , SA vuông góc với đáy , AB=2AB=4a . tính thể tích khối chóp S.ABCD .biết rằng góc giữa mặt phẳng (SBD) và (ABCD) = 30 độ
Theo dõi (1) 2 Trả lời -
cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a . hình chiếu vuông góc của A' xuống mặt phẳng (ABC) là trung điểm của AB . Mặt bên (AA'C'C) tạo với đáy một góc 45 độ. tính thể tích khối lăng trụ
Theo dõi (0) 4 Trả lời -
cho hình trụ có thiết diện qua trục là hình vuông cạnh a, thể tích của khối lăng trụ tứ giác đều ngoại tiếp hình trụ là?
Theo dõi (0) 5 Trả lời -
Tính thể tích khối chóp S.ABC biết khoảng cách từ A đến (MBC) bằng 6a/căn21
bởi Trần Khánh Duy
03/12/2018
Cho hình chóp S.ABC có đáy là ABC là tam giác đèu cạnh 2a. Gọi M là trung điểm của SA, góc SAB= góc SCB= 90°. Biết khoảng cách từ A đến (MBC) bằng 6a/căn21. Tính thể tích khối chóp S.ABC
Theo dõi (1) 2 Trả lời -
Tính khoảng cách giữa OG với AD biết góc giữa SC với (ABCD) bằng 45 độ
bởi nguyễn thị nhị
30/11/2018
Cho hình chóp SABCD có đáy là hình vuông cạnh a tâm O SA vuông góc với đáy Góc giữa SC với (ABCD) 45 độ Có G là trọng tâm của SCD tính khoảng cách giữa OG với AD mong mọi người giúp mk với
Theo dõi (0) 3 Trả lời -
Tính khoảng cách giữa SB và AC biết hình chóp S.ABCD có đáy hình thang vuông tại A và B, AB=BC=2, AD=4
bởi Hồ Hoàng Khiêm
26/11/2018
cho hình chóp S.ABCD có đáy hình thang vuông tại A và B. AB=BC=2,AD=4. SA vuông với đáy ; góc giữa mặt phẳng (SCD) với đáy bằng một góc 45o . Tính khoảng cách giữa SB và AC
Theo dõi (1) 3 Trả lời -
Chiều cao x của khối nón này là bao nhiêu để thể tích của nó lớn nhất ?
bởi Hồ Hoàng Khiêm
26/11/2018
cho hình nốn tâm O, chiều cao là h.Một hình nón khác có đỉnh là tâm của của đáy và đáy là một thiết diện song song với đáycủa hình nón đã cho .Chiều cao x của khối nón này là bao nhiêu để thể tích của nó lớn nhất
Theo dõi (0) 3 Trả lời -
Tính khoảng cách từ điểm C đến mp SAB biết S.ABC có đáy ABC là tam giác vuông cân tại A
bởi Quỳnh Trang
15/11/2018
Chóp S.ABC có đáy ABC là tam giác vuông cân tại A, mẶt bên SBC là tam giác đều cạnh a và mặt phẳng SBC vuống góc đáy. Khoảng cách từ điểm C đến mp SAB là??
Theo dõi (0) 2 Trả lời -
Tính khoảng cách từ điểm B đến mặt phẳng (SMC) biết hình chóp S.ABC có đáy ABC là tam giác đều cạnh a
bởi Nguyệt Vũ
13/11/2018
Caau1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC); góc giữa đường thẳng SB và mặt phẳng (ABC) bằng 60o. Gọi M là trung điểm của cạnh AB. Tính khoảng cách từ điểm B đến mặt phẳng (SMC).
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AC = 2a, BC = a. Đỉnh S cách đều các điểm A, B, C. Tính khoảng cách từ trung điểm M của SC đến mặt phẳng (SBD).
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AD=2BC, AB = BC = a căn3 .Đường thẳng SA vuông góc với mặt phẳng (ABCD). Gọi E là trung điểm của cạnh SC. Tính khoảng cách từ điểm E đến mặt phẳng (SAD).
Theo dõi (0) 2 Trả lời -
Tính thể tích khối chóp A'BCC'B' biết hình lăng trụ ABCD.A'B'C'D' có đáy ABC là tam giác đều cạnh a
bởi Lạnh Lùng Nhók
02/11/2018
cho hình lăng trụ abc.a'b'c' có đáy abc là tam giác đều cạnh a, cạnh bên bằng b và hợp với đáy góc 60 độ, tính thể tích khối chóp A'BCC'B'
Theo dõi (1) 4 Trả lời -
Tính theo a khoảng cách giữa AB' và A'C' biết hình hộp ABCD.A'B'C'D' có A'.ABD là hình chóp đều
bởi Dinh Thi Thu Ha
28/10/2018
Cho hình hộp ABCD.A'B'C'D' có A'.ABD là hình chóp đều, AB=AA'=a. Tính theo a khoảng cách giữa hai đường thảng AB' VÀ A'C'
EM CẢM ƠN!
Theo dõi (0) 0 Trả lời -
Tính góc giữa BG và SA biết hình chóp tứ giác đều S.ABCD có AB=a, SA=a.căn 3
bởi Hồ Phương Trinh
11/10/2018
1/ cho hình chóp tg đều S.ABCD CÓ AB=a, SA=a.(căn 3). Gọi G là trọng tâm tam giác SCD. GÓC GIỮA ĐThang BG vs SA =?
A. arccos(căn 330)/110
B. arccos(căn 33)/11
C. arccos(căn 3)/11
D. arccos(căn 33)/22
Theo dõi (0) 1 Trả lời
