OPTADS360
ATNETWORK
RANDOM
ON
YOMEDIA
Banner-Video
IN_IMAGE

Bài tập 1.16 trang 19 SBT Hình học 12

Lý thuyết10 Trắc nghiệm

25 BT SGK

585 FAQ

Giải bài 1.16 tr 19 SBT Hình học 12

Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB = a, BC = b, AA′ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB′ và DD′ sao cho \(BE = \frac{1}{2}EB',DF = \frac{1}{2}FD'\). Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A′B′C′D′ thành hai khối đa diện (H) và (H′). Gọi (H′) là khối đa diện chứa đỉnh A′. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H′).

AMBIENT-ADSENSE/lession_isads=0
QUẢNG CÁO
 

Hướng dẫn giải chi tiết

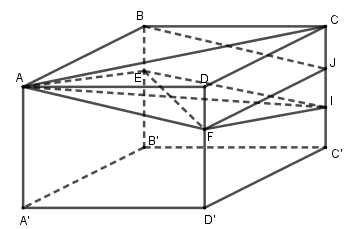
Gọi \(I = CC' \cap \left( {AEF} \right)\)

Vì \(\left\{ {\begin{array}{*{20}{l}}
{\left( {AEF} \right) \cap \left( {ABB'A'} \right) = AE}\\
{\left( {AEF} \right) \cap \left( {CDD'C'} \right) = FI}\\
{\left( {ABB'A'} \right)\parallel \left( {CDD'C'} \right)}
\end{array}} \right.\) 

Nên AE // FI.

Tương tự AF // EI nên tứ giác AEIF là hình bình hành.

Trên cạnh C lấy điểm J sao cho CJ = DF.

Dễ thấy FJ // CD // AB, FI = CD = AB 

Nên ABJF là hình bình hành \( \Rightarrow AF//BJ,AF = BJ\).

Suy ra EI // BJ, EI = BJ hay EBJI là hình bình hành \( \Rightarrow BE = JI\).

Từ đó suy ra \(IJ = EB = DF = JC = \frac{c}{3}\)

Ta có \({S_{BCIE}} = \frac{1}{2}\left( {\frac{{c + 2c}}{3}} \right)b = \frac{{bc}}{2},\)

\({S_{DCIF}} = \frac{1}{2}\left( {\frac{{c + 2c}}{3}} \right)a = \frac{{ac}}{2}\)

Nên \({V_{(H)}} = {V_{A.BCIE}} + {V_{A.DCIF}} \)

\(= \frac{1}{3}.\frac{{bc}}{2}.a + \frac{1}{3}.\frac{{ac}}{2}.b = \frac{{abc}}{3}\)

Lại có:

\({V_{ABCD.A'B'C'D'}} = abc \Rightarrow {V_{(H')}} = \frac{2}{3}abc\)

\( \Rightarrow \frac{{{V_{(H)}}}}{{{V_{(H')}}}} = \frac{1}{2}\)

-- Mod Toán 12 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 1.16 trang 19 SBT Hình học 12 HAY thì click chia sẻ 
 
 

Bài tập SGK khác

Bài tập 1.14 trang 18 SBT Hình học 12

Bài tập 1.15 trang 19 SBT Hình học 12

Bài tập 1.17 trang 19 SBT Hình học 12

Bài tập 15 trang 28 SGK Hình học 12 NC

Bài tập 16 trang 28 SGK Hình học 12 NC

Bài tập 17 trang 28 SGK Hình học 12 NC

Bài tập 18 trang 28 SGK Hình học 12 NC

Bài tập 19 trang 28 SGK Hình học 12 NC

Bài tập 20 trang 28 SGK Hình học 12 NC

Bài tập 21 trang 28 SGK Hình học 12 NC

Bài tập 22 trang 28 SGK Hình học 12 NC

Bài tập 23 trang 29 SGK Hình học 12 NC

Bài tập 24 trang 29 SGK Hình học 12 NC

Bài tập 25 trang 29 SGK Hình học 12 NC

NONE
OFF

XEM NHANH CHƯƠNG TRÌNH LỚP 12