Giải bài 3.42 tr 131 SBT Hình học 12
Cho hai đường thẳng: \(d:\frac{{x - 1}}{{ - 1}} = \frac{{y - 2}}{2} = \frac{z}{3}\) và \(d':\left\{ {\begin{array}{*{20}{c}}
{x = 1 + t'}\\
{y = 3 - 2t'}\\
{z = 1}
\end{array}} \right.\)
Lập phương trình đường vuông góc chung của d và d’.
Hướng dẫn giải chi tiết
Phương trình tham số của đường thẳng \(\left\{ {\begin{array}{*{20}{c}}
{x = 1 - t}\\
{y = 2 + 2t}\\
{z = 3t}
\end{array}} \right.\)
Vecto chỉ phương của hai đường thẳng d và d’ lần lượt là \(\vec a = ( - 1;2;3),\overrightarrow {a'} = (1; - 2;0)\)
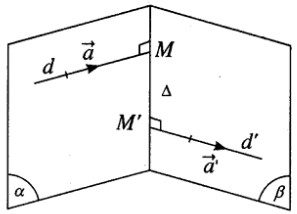
Xét điểm M(1 – t; 2 + 2t; 3t) trên d và điểm M’(1 + t’; 3 – 2t’ ; 1) trên d’ ta có \(\overrightarrow {MM'} = (t' + t;1 - 2t' - 2t;1 - 3t)\)
MM’ là đường vuông góc chung của d và d’.
\(\begin{array}{l}
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{\overrightarrow {MM'} .\vec a = 0}\\
{\overrightarrow {MM'} .\overrightarrow {a'} = 0}
\end{array}} \right.\\
\Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{ - t' - t + 2 - 4t' - 4t + 3 - 9t = 0}\\
{t' + t - 2 + 4t' + 4t = 0}
\end{array}} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
5t\prime + 14t = 5\\
5t\prime + 5t = 2
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
t = \frac{1}{3}\\
t' = \frac{1}{{15}}
\end{array} \right.
\end{array}\)
Thay giá trị của t và t’ vào ta được tọa độ M và M’ là \(M\left( {\frac{2}{3};\frac{8}{3};1} \right),M'\left( {\frac{{16}}{{15}};\frac{{43}}{{15}};1} \right)\)
Do đó \(\overrightarrow {MM'} = \left( {\frac{6}{{15}};\frac{3}{{15}};0} \right)\)
Suy ra đường vuông góc chung Δ của d và d’ có vecto chỉ phương \(\vec u = (2;1;0)\)
Vậy phương trình tham số của Δ là: \(\left\{ {\begin{array}{*{20}{c}}
{x = \frac{2}{3} + 2t}\\
{y = \frac{8}{3} + t}\\
{z = 1}
\end{array}} \right.\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.39 trang 130 SBT Hình học 12
Bài tập 3.40 trang 130 SBT Hình học 12
Bài tập 3.43 trang 131 SBT Hình học 12
Bài tập 3.44 trang 131 SBT Hình học 12
Bài tập 3.45 trang 131 SBT Hình học 12
Bài tập 24 trang 102 SGK Hình học 12 NC
Bài tập 25 trang 102 SGK Hình học 12 NC
Bài tập 26 trang 102 SGK Hình học 12 NC
Bài tập 27 trang 103 SGK Hình học 12 NC
Bài tập 28 trang 103 SGK Hình học 12 NC
Bài tập 29 trang 103 SGK Hình học 12 NC
Bài tập 30 trang 103 SGK Hình học 12 NC
Bài tập 31 trang 103 SGK Hình học 12 NC
Bài tập 32 trang 104 SGK Hình học 12 NC
Bài tập 33 trang 104 SGK Hình học 12 NC
-


Tính bán kính R của mặt cầu (S) biết (S) có tâm I và cắt (P) theo một đường tròn (T)
bởi Ma Phương Ma
 04/04/2020
trong không gian với hệ trục tọa độ oxyz, cho điểm i(-2,1,3) và mặt phẳng (p) :2x-y 2z-10=0. tính bán kính r của mặt cầu (s) , biết rằng (s) có tâm i và nó cắt (p) theo một đường tròn (t) có chu vi bằng 10πTheo dõi (1) 1 Trả lời
04/04/2020
trong không gian với hệ trục tọa độ oxyz, cho điểm i(-2,1,3) và mặt phẳng (p) :2x-y 2z-10=0. tính bán kính r của mặt cầu (s) , biết rằng (s) có tâm i và nó cắt (p) theo một đường tròn (t) có chu vi bằng 10πTheo dõi (1) 1 Trả lời -


Trong không gian Oxyz, cho điểm A thuộc (P): 3x+11y-4z+17=0, B là điểm trên đường thẳng ∆: (x-1)/-1=(y-7)/10=(z+4)/-8 và C(-6;19;-22). Tính OA biết G(-3;6;-4) là trọng tâm tam giác ABC.
bởi Lê Lê
 26/03/2020
26/03/2020
 Theo dõi (1) 8 Trả lời
Theo dõi (1) 8 Trả lời -


Trong không gian, viết phương trình đường thẳng đi qua điểm A và vuông góc với mặt phẳng (P): 4x 3y-7z +1=0
bởi Ly Nguyễn
 25/03/2020
, đường thẳng đi qua điểm A và vuông góc với mặt phẳng (P): 4x 3y-7z 1=0Theo dõi (0) 3 Trả lời
25/03/2020
, đường thẳng đi qua điểm A và vuông góc với mặt phẳng (P): 4x 3y-7z 1=0Theo dõi (0) 3 Trả lời -


Phương trình mặt phẳng (α) đi qua điểm M(-1;-2;1) và song song với mặt phẳng Oxz
bởi Thương Em
 22/03/2020
Mọi người giải giúp mjk từ câu 30 trở đi với ạ mjk chưa biết cách giải.
22/03/2020
Mọi người giải giúp mjk từ câu 30 trở đi với ạ mjk chưa biết cách giải. Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -
ADMICRO


Trong không gian Oxyz, tìm trên Ox điểm A cách đều đường thẳng d: (x-1)/1=y/2=(z+2)/2 và mặt phẳng (P): 2x-y-2z=0
bởi Le Anh
 09/03/2020
09/03/2020
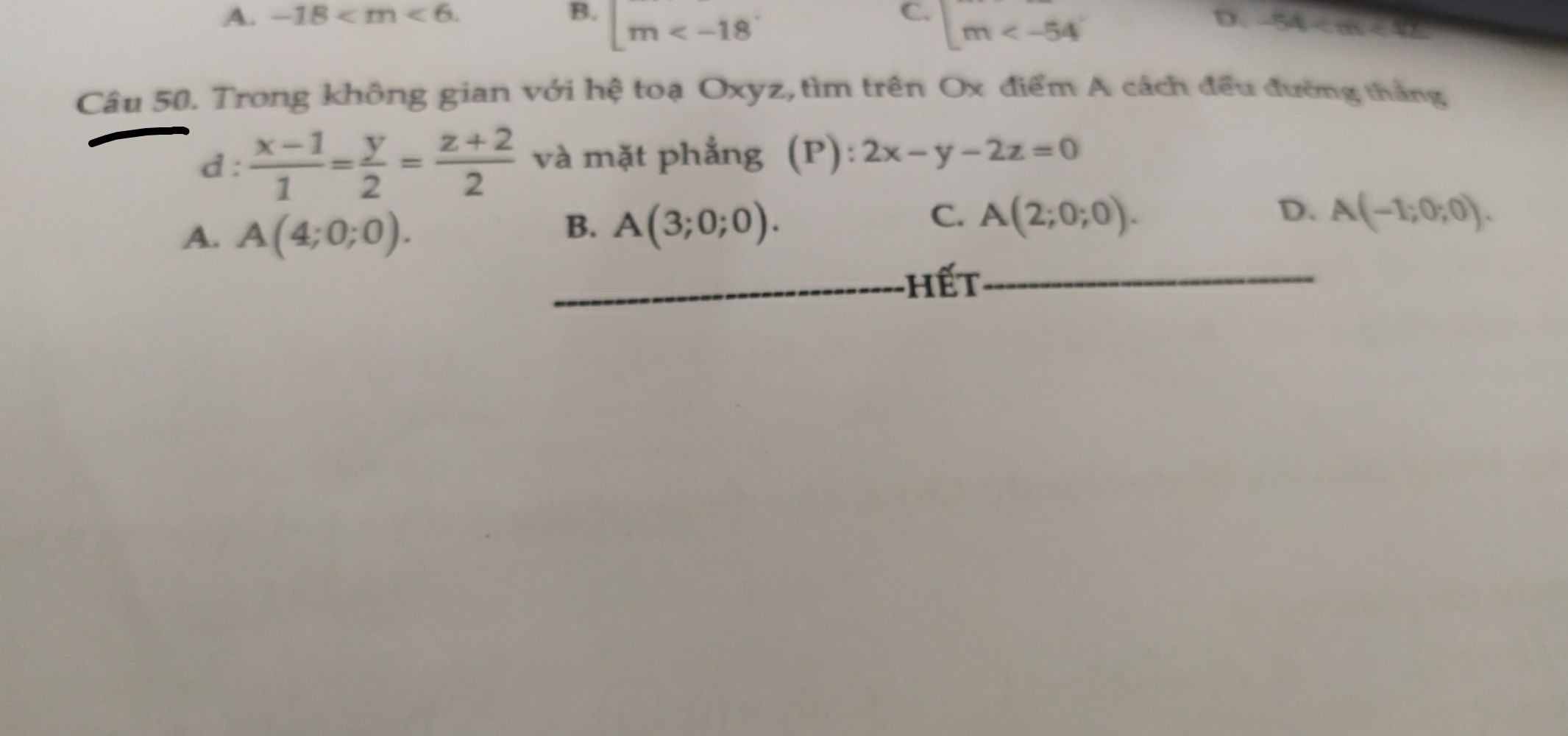 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Cho A(1;0;0) B(0;2;0) và mặt phẳng (P) : x y 2z 3=0. Tìm M thuộc mặt phẳng (P) sao cho (MA MB )đạt minTheo dõi (1) 5 Trả lời
Cho A(1;0;0) B(0;2;0) và mặt phẳng (P) : x y 2z 3=0. Tìm M thuộc mặt phẳng (P) sao cho (MA MB )đạt minTheo dõi (1) 5 Trả lời


