Giải bài 3.40 tr 130 SBT Hình học 12
Cho điểm M(2; -1; 1) và đường thẳng \({\rm{\Delta }}:\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{z}{2}\)
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên đường thẳng Δ;
b) Tìm tọa độ điểm M’ đối xứng với M qua đường thẳng Δ.
Hướng dẫn giải chi tiết
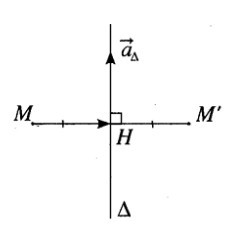
a) Phương trình tham số của \({\rm{\Delta }}:\left\{ {\begin{array}{*{20}{c}}
{x = 1 + 2t}\\
{y = - 1 - t}\\
{z = 2t}
\end{array}} \right.\)
Xét điểm \(H(1 + 2t; - 1 - t;2t) \in {\rm{\Delta }}\)
Ta có \(\overrightarrow {MH} = (2t - 1; - t;2t - 1)\)
\(\overrightarrow {{a_{\rm{\Delta }}}} = (2; - 1;2)\)
H là hình chiếu vuông góc của M trên \({\rm{\Delta }} \Leftrightarrow \overrightarrow {MH} .\overrightarrow {{a_{\rm{\Delta }}}} = 0\)
\( \Leftrightarrow 2(2t - 1) + t + 2(2t - 1) = 0 \Leftrightarrow t = \frac{4}{9}\)
Ta suy ra tọa độ điểm \(H\left( {\frac{{17}}{9};\frac{{ - 13}}{9};\frac{8}{9}} \right)\)
b) H là trung điểm của MM’, suy ra xM’ + xM = 2xH
Suy ra \({x_{M'}} = 2{x_H} - {x_M} = \frac{{34}}{9} - 2 = \frac{{16}}{9}\)
Tương tự, ta được \({y_{M'}} = 2{y_H} - {y_M} = \frac{{ - 26}}{9} + 1 = \frac{{ - 17}}{9};\)
\({z_{M'}} = 2{z_H} - {z_M} = \frac{{16}}{9} - 1 = \frac{7}{9}\)
Vậy \(M'\left( {\frac{{16}}{9};\frac{{ - 17}}{9};\frac{7}{9}} \right)\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
Bài tập 3.38 trang 130 SBT Hình học 12
Bài tập 3.39 trang 130 SBT Hình học 12
Bài tập 3.42 trang 131 SBT Hình học 12
Bài tập 3.43 trang 131 SBT Hình học 12
Bài tập 3.44 trang 131 SBT Hình học 12
Bài tập 3.45 trang 131 SBT Hình học 12
Bài tập 24 trang 102 SGK Hình học 12 NC
Bài tập 25 trang 102 SGK Hình học 12 NC
Bài tập 26 trang 102 SGK Hình học 12 NC
Bài tập 27 trang 103 SGK Hình học 12 NC
Bài tập 28 trang 103 SGK Hình học 12 NC
Bài tập 29 trang 103 SGK Hình học 12 NC
Bài tập 30 trang 103 SGK Hình học 12 NC
Bài tập 31 trang 103 SGK Hình học 12 NC
Bài tập 32 trang 104 SGK Hình học 12 NC
Bài tập 33 trang 104 SGK Hình học 12 NC
-


Xét vị trí tương đối của hai đường thẳng d1 và d2?
bởi vinh Khiêm
 30/04/2020
Giúp em câu này với ạk
30/04/2020
Giúp em câu này với ạk Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Chứng minh \( \Delta // \Delta '\)??
bởi Trọng Huy
 29/04/2020
29/04/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Viết phương trình tham số của các đường thẳng d đi qua 2 điểm A(2;-3;5), B(1;-2;3)
bởi Vy Vy
 29/04/2020
29/04/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Viết phương trình mặt phẳng (P) đi qua M(1;-2; 3) và nhận vecto n=(2;1;-5) làm VTPT
bởi Ngọc Burrin
 26/04/2020
26/04/2020
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -
ADMICRO


Tính môđun của số phức liên hợp z biết z=2+3i
bởi Mi Mi
 22/04/2020
22/04/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm tập hợp các điểm M(x,y,z) nằm trên mặt phẳng (P) sao cho tam giác MAB có diện tích nhỏ nhất
bởi Cherverlet Olando
 17/04/2020
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( P ) : 3 x y − z 5 = 0 P 3 x y z 5 0 và hai điểm A(1;0;2), B(2;-1;4). Tìm tập hợp các điểm M(x,y,z) nằm trên mặt phẳng (P) sao cho tam giác MAB có diện tích nhỏ nhất.Theo dõi (0) 0 Trả lời
17/04/2020
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( P ) : 3 x y − z 5 = 0 P 3 x y z 5 0 và hai điểm A(1;0;2), B(2;-1;4). Tìm tập hợp các điểm M(x,y,z) nằm trên mặt phẳng (P) sao cho tam giác MAB có diện tích nhỏ nhất.Theo dõi (0) 0 Trả lời


