Bài tập 10 trang 40 SGK Hình học 12

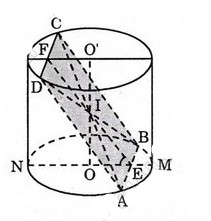
Do tính chất đối xứng của (ABCD) nên (ABCD) cắt OO′ tại trung điểm I của OO′. I cũng là giao điểm của hai đường chéo AC, BD

Xét tam giác vuông IOB ta có: IB²=IO²+OB²

\(\begin{array}{l}
 \Rightarrow IB = \sqrt {{{\left( {\frac{r}{2}} \right)}^2} + {r^2}}  = \frac{{r\sqrt 5 }}{2}\\
 \Rightarrow AC = BD = 2IB = r\sqrt 5 
\end{array}\)

Do ABCD là hinh vuông nên \(AB = \frac{{AC}}{{\sqrt 2 }} = \frac{{r\sqrt {10} }}{2}\)

Vậy \({S_{ABCD}} = A{B^2} = \frac{{5{r^2}}}{2}\)

Gọi E là trung điểm của AB

⇒ OE ⊥ AB, IE ⊥ AB

\( \Rightarrow \widehat {IEO}\) là góc giữa (ABCD)$(ABCD)$  và mặt đáy của hình trụ.

Ta có: \(IE = \frac{1}{2}AD = \frac{{r\sqrt {10} }}{4},OI = \frac{r}{2}\)

Xét tam giác vuông IOE có: 

\(\begin{array}{l}
OE = \sqrt {I{E^2} - O{I^2}} \\
 = \sqrt {{{\left( {\frac{{r\sqrt {10} }}{4}} \right)}^2} - {{\left( {\frac{r}{2}} \right)}^2}}  = \frac{{r\sqrt 6 }}{4}\\
\cos \widehat {IEO} = \frac{{OE}}{{IE}} = \frac{{\sqrt {15} }}{5}
\end{array}\)

-- Mod Toán 12 HỌC247