Phần hướng dẫn giải bài tập SGK bài 1 Định nghĩa và ý nghĩa của đạo hàm sẽ giúp các em nắm được phương pháp và rèn luyện kĩ giải các bài tập tính đạo hàm bằng định nghĩa, viết phương trình tiếp tuyến của đồ thị hàm số, giải bài toán vật lý bằng cách sử dụng đạo hàm,...từ SGK Đại số và Giải tích 11 Cơ bản và Nâng cao.
-
Bài tập 1 trang 156 SGK Đại số & Giải tích 11
Tìm số gia của hàm số \(f(x) = x^3\), biết rằng :
a) \(x_0 = 1; \Delta x = 1\)
b) \(x_0 = 1; \Delta x = -0,1\)
-
Bài tập 2 trang 156 SGK Đại số & Giải tích 11
Tính \(\Delta y\) và \(\frac{{\Delta y}}{{\Delta x}}\) của các hàm số sau theo x và \(\Delta x\) :
a) \(y = 2x - 5\);
b) \(y = x^2 - 1\);
c) \(y = 2x^3\);
d) \(y = \frac{1}{x}\).
-
Bài tập 3 trang 156 SGK Đại số & Giải tích 11
Tính (bằng định nghĩa) đạo hàm của mỗi hàm số sau tại các điểm đã chỉ ra:
a) \(y = x^2 + x\) tại \(x_0 = 1\);
b) \(y = \frac{1}{x}\) tại \(x_0 = 2\);
c) \(y =\frac{x+1}{x-1}\) tại \(x_0 = 0\).
-
Bài tập 4 trang 156 SGK Đại số & Giải tích 11
Chứng minh rằng hàm số \(f(x) = (x - 1)^2\) nếu \(x \geq 0\) và \(f(x) = -x^2\) nếu \(x < 0\)
không có đạo hàm tại điểm \(x = 0\) nhưng có đạo hàm tại điểm \(x = 2\).
- VIDEOYOMEDIA
-
Bài tập 5 trang 156 SGK Đại số & Giải tích 11
Cho đường cong \(y = x^3.\) Viết phương trình tiếp tuyến của đường cong trong các trường hợp:
a) Tại điểm có tọa độ (-1;-1);
b) Tại điểm có hoành độ bằng 2;
c) Biết hệ số góc của tiếp tuyến bằng 3.
-
Bài tập 6 trang 156 SGK Đại số & Giải tích 11
Viết phương trình tiếp tuyến của đường hypebol \(y =\frac{1}{x}\):
a) Tại điểm \((\frac{1}{2} ; 2)\)
b) Tại điểm có hoành độ bằng -1;
c) Biết rằng hệ số góc của tiếp tuyến bằng \(- \frac{1}{4}\).
-
Bài tập 7 trang 157 SGK Đại số & Giải tích 11
Một vật rơi tự do theo phương trình \(s=\frac{1}{2}gt^2,\) trong đó g ≈ 9,8 m/s2 là gia tốc trọng trường.
a) Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t=5s) đến t + ∆t, biết rằng ∆t = 0,1s; ∆t = 0,05s; ∆t = 0,001s.
b) Tìm vận tốc tức thời của chuyển động tại thời điểm t = 5s.
-
Bài tập 5.1 trang 198 SBT Toán 11
Sử dụng định nghĩa, hãy tìm đạo hàm của các hàm số sau:
a) \(y = 3x - 5\)
b) \(y = 4{x^2} - 0,6x + 7\)
c) \(y = 4x - {x^2}\)
d) \(y = \sqrt {3x + 1} \)
e) \(y = \frac{1}{{x - 2}}\)
f) \(y = \frac{{1 + \sqrt x }}{{1 - \sqrt x }}\)
-
Bài tập 5.2 trang 198 SBT Toán 11
Cho \(f(x) = \sqrt[3]{{x - 1}}\). Tính f′(0), f′(1)
-
Bài tập 5.3 trang 198 SBT Toán 11
Cho \(\varphi (x) = \frac{8}{x}\). Chứng minh rằng \(\varphi '( - 2) = \varphi '(2)\)
-
Bài tập 5.4 trang 198 SBT Toán 11
Chứng minh rằng hàm số \(y = |x - 1|\) không có đạo hàm tại , nhưng liên tục tại điểm đó.
-
Bài tập 5.5 trang 198 SBT Toán 11
Chứng minh rằng hàm số
\(y = signx = \left\{ \begin{array}{l}
1,\,\,\,\,\,\,x > 0\\
0,\,\,\,\,\,\,x = 0\\
- 1,\,\,\,\,x < 0
\end{array} \right.\)không có đạo hàm tại x = 0.
-
Bài tập 5.6 trang 198 SBT Toán 11
Viết phương trình tiếp tuyến của đồ thị các hàm số
a) \(y = {x^3} - 3{x^2} + 2\) tại điểm (−1;−2)
b) \(y = {x^4} - 2{x^2}\) tại điểm có hoành độ x = −2
c) \(y = \frac{{2x + 1}}{{x - 2}}\) biết hệ số góc của tiếp tuyến bằng −5
-
Bài tập 5.7 trang 199 SBT Toán 11
Cho \(f(x) = 3{x^2} - 4x + 9\)
Tìm \(\frac{{{\rm{\Delta }}f(x)}}{{{\rm{\Delta }}x}}\) tại
A. \(2 - 3{\rm{\Delta }}x\)
B. \(2 + 3{\rm{\Delta }}x\)
C. \(1 + 3{\rm{\Delta }}x\)
D. \( - 2 + 5{\rm{\Delta }}x\)
-
Bài tập 5.8 trang 199 SBT Toán 11
Cho hàm số \(y = \sin 2x\). Tìm \(\frac{{{\rm{\Delta }}y}}{{{\rm{\Delta }}x}}\) tại \(x = \frac{\pi }{4}\)
A. \(\frac{{ - 2{{\sin }^2}{\rm{\Delta }}x}}{{{\rm{\Delta }}x}}\)
B. \(\frac{{{{\sin }^{}}{\rm{\Delta }}x}}{{{\rm{\Delta }}x}}\)
C. \(\frac{{2{{\sin }^2}{\rm{\Delta }}x}}{{{\rm{\Delta }}x}}\)
D. \(\frac{{3{{\sin }^2}{\rm{\Delta }}x}}{{{\rm{\Delta }}x}}\)
-
Bài tập 5.9 trang 199 SBT Toán 11
Cho hàm số \(y = \left\{ \begin{array}{l}
x,\,\,\,\,x < 0\\
{x^2},\,\,x \ge 0
\end{array} \right.\)
Hãy tínha) \(\mathop {\lim }\limits_{{\rm{\Delta }}x \to {0^ + }} \frac{{{\rm{\Delta }}y}}{{{\rm{\Delta }}x}}\) tại
b) \(\mathop {\lim }\limits_{{\rm{\Delta }}x \to {0^ - }} \frac{{{\rm{\Delta }}y}}{{{\rm{\Delta }}x}}\) tại
A. a) -1 và b) 1 B. a) 1 và b) 1 C. a) 0 và b) 0 D. a) 0 và b) 1 -
Bài tập 5.10 trang 199 SBT Toán 11
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{{{x^2} + 4x + 5}}{{x + 2}}\) tại điểm có hoành độ
A. \(y = \frac{3}{4}x - \frac{5}{2}\)
B. \(y = x + \frac{5}{2}\)
C. \(y = \frac{3}{4}x + 1\)
D. \(y = \frac{3}{4}x + \frac{5}{2}\)
-
Bài tập 5.11 trang 199 SBT Toán 11
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \sqrt {2x + 1} \) biết hệ số góc của tiếp tuyến bằng \(\frac{1}{3}\)
A. \(y = \frac{x}{2} + \frac{5}{3}\)
B. \(y = \frac{x}{3} - \frac{5}{3}\)
C. \(y = \frac{x}{3} + \frac{5}{3}\)
D. \(y = x - 1\)
Lời giải: -
Bài tập 1 trang 192 SGK Toán 11 NC
Tìm số gia của hàm số y = x2 − 1 tại điểm x0 = 1 ứng với số gia ∆x, biết
a. ∆x = 1
b. ∆x = -0,1.
-
Bài tập 2 trang 192 SGK Toán 11 NC
Dùng định nghĩa, tính đạo hàm của mỗi hàm số sau tại điểm x0
\(\begin{array}{l}
a)\,\,y = 2x + 1,{x_0} = 2\\
b)\,\,y = {x^2} + 3x,{x_0} = 1
\end{array}\) -
Bài tập 3 trang 192 SGK Toán 11 NC
Dùng định nghĩa, tính đạo hàm của mỗi hàm số sau tại điểm x0 (a là hằng số)
a) y = ax + 3
b) \(y = \frac{1}{2}a{x^2}\)
-
Bài tập 4 trang 192 SGK Toán 11 NC
Cho parabol y = x2 và hai điểm A(2 ; 4) và B(2 + ∆x ; 4 + ∆y) trên parabol đó.
a. Tính hệ số góc của cát tuyến AB biết ∆x lần lượt bằng 1 ; 0,1 và 0,01.
b. Tính hệ số góc của tiếp tuyến của parabol đã cho tại điểm A.
-
Bài tập 5 trang 192 SGK Toán 11 NC
Viết phương trình tiếp tuyến của đồ thị hàm số y = x3, biết
a. Tiếp điểm có hoành độ bằng -1
b. Tiếp điểm có tung độ bằng 8
c. Hệ số góc của tiếp tuyến bằng 3.
-
Bài tập 6 trang 192 SGK Toán 11 NC
Một vật rơi tự do có phương trình chuyển động là \(S = \frac{1}{2}g{t^2}\) , trong đó g = 9,8m/s2 và t được tính bằng giây (s).
a. Tìm vận tốc trung bình trong khoảng thời gian từ t đến t + ∆t với độ chính xác 0,001, biết t = 5 và ∆t lần lượt bằng 0,1 ; 0,01 ; 0,001.
b. Tìm vận tốc tại thời điểm t = 5.
-
Bài tập 7 trang 192 SGK Toán 11 NC
Tìm đạo hàm của hàm số f(x) = x5 trên R rồi suy ra f′(−1), f′(−2) và f′(2)
-
Bài tập 8 trang 192 SGK Toán 11 NC
Tìm đạo hàm của mỗi hàm số sau trên R.
a. y = ax2 (a là hằng số)
b. y = x3 + 2
-
Bài tập 9 trang 192 SGK Toán 11 NC
Tính đạo hàm của mỗi hàm số sau :
a) \(y = \frac{1}{{2x - 1}}\) với \(x \ne \frac{1}{2}\)
b) \(y = \sqrt {3 - x} \) với x < 3
-
Bài tập 10 trang 195 SGK Toán 11 NC
a. Tính f′(3) và f′(−4) nếu f(x) = x3
b. Tính f′(1) và f′(9) nếu \(f(x) = \sqrt x \)
-
Bài tập 11 trang 195 SGK Toán 11 NC
Cho hàm số y = f(x) có đạo hàm tại điểm x0 và đồ thị (G). Mệnh đề sau đây đúng hay sai ?
a. Nếu f′(x0) = 0 thì tiếp tuyến của (G) tại điểm M(x0; f(x0)) song song với trục hoành.
b. Nếu tiếp tuyến của G tại điểm M(x0; f(x0)) song song với trục hoành thì f′(x0) = 0
-
Bài tập 12 trang 195 SGK Toán 11 NC
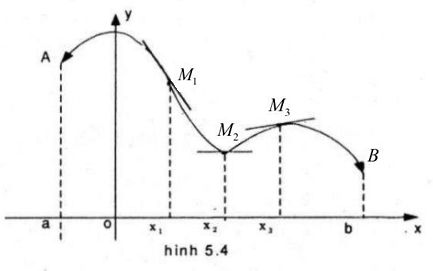
Hình 5.4 là đồ thị của hàm số y = f(x) trên khoảng (a ; b). Biết rằng tại các điểm M1, M2 và M3, đồ thị hàm số có tiếp tuyến được thể hiện trên hình vẽ. Dựa vào hình vẽ, em hãy nêu nhận xét về dấu của f′(x1), f′(x2) và f′(x3)
-
Bài tập 13 trang 195 SGK Toán 11 NC
Chứng minh rằng để đường thẳng y = ax + b là tiếp tuyến của đồ thị hàm số y = f(x) tại điểm (x0; f(x0)), điều kiện cần và đủ là \(\left\{ \begin{array}{l}
a = f\prime ({x_0})\\
a{x_0} + b = f({x_0})
\end{array} \right.\) -
Bài tập 14 trang 195 SGK Toán 11 NC
Cho hàm số y = |x|
a. Chứng minh rằng hàm số đã cho liên tục tại điểm x = 0
b. Tính đạo hàm của hàm số tại x = 0, nếu có.
c. Mệnh đề “Hàm số liên tục tại điểm x0 thì có đạo hàm tại x0 ” đúng hay sai ?
-
Bài tập 15 trang 195 SGK Toán 11 NC
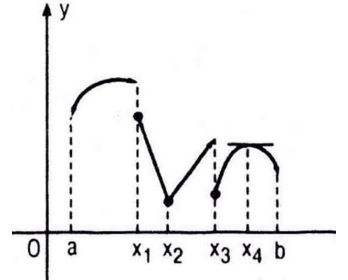
Hình 5.5 là đồ thị của hàm số y = f(x) xác định trên khoảng (a ; b). Dựa vào hình vẽ, hãy cho biết tại mỗi điểm x1, x2, x3 và x4:
a. Hàm số có liên tục hay không ?
b. Hàm số có đạo hàm hay không ? Hãy tính đạo hàm nếu có.