Giải bài 6 tr 156 sách GK Toán ĐS & GT lớp 11
Viết phương trình tiếp tuyến của đường hypebol \(y =\frac{1}{x}\):
a) Tại điểm \((\frac{1}{2} ; 2)\)
b) Tại điểm có hoành độ bằng -1;
c) Biết rằng hệ số góc của tiếp tuyến bằng \(- \frac{1}{4}\).
Hướng dẫn giải chi tiết bài 6
Phương pháp:
Các bước viết phương trình tiếp tuyến của đồ thị (C) của hàm số y=f(x) tại điểm \(M_0(x_0;y_0) \in (C):\)
Bước 1: Tính \(f'({x_0}) = \mathop {\lim }\limits_{ x \to x_0} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}= \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f({x_0} + \Delta x) - f({x_0})}}{{x - {x_0}}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}.\)
Bước 2: Hệ số góc của tiếp tuyến với đồ thị (C) tại \(M_0\) là \(k=f'(x_0)\)
Bước 3: Phương trình tiếp tuyến với đồ thị (C) tại điểm \(M_0(x_0;y_0) \in (C)\) là: \(y = f'({x_0}).(x - {x_0}) + {y_0}\)
Viết phương trình tiếp tuyến của đồ thị (C) hàm số y=f(x) khi biết hệ số k, ta thực hiện các bước sau:
Bước 1: Gọi \(M_0(x_0;y_0) \in (C)\) là tiếp điểm của tiếp tuyến với đồ thị (C).
Bước 2: Tính \(f'({x_0}) = \mathop {\lim }\limits_{ x \to x_0} \frac{{f(x) - f({x_0})}}{{x - {x_0}}}= \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f({x_0} + \Delta x) - f({x_0})}}{{x - {x_0}}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}.\)
Bước 3: Giải phương trình \(k=f'(x_0)\) tìm \(x_0\), rồi tìm \(y_0=f(x_0).\)
Bước 4: Phương trình tiếp tuyến của đồ thị (C) với hệ số góc k là: \(y = k(x - {x_0}) + {y_0}.\)
Lời giải:
Lời giải chi tiết câu a, b, c bài 6 như sau:
\(\begin{array}{l} y = \frac{1}{x}\\ \Delta y = \frac{1}{{x + \Delta x}} - \frac{1}{x} = \frac{{x - (x + \Delta x)}}{{x\left( {x + \Delta x} \right)}} = - \frac{{\Delta x}}{{{x^2} + x.\Delta x}}\\ \frac{{\Delta y}}{{\Delta x}} = - \frac{1}{{{x^2} + x.\Delta x}}\\ y'(x) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = - \frac{1}{{{x^2}}} \end{array}\)
Câu a:
Tại \(x_0=\frac{1}{2}\Rightarrow y'(\frac{1}{2})=-4\)
⇒ Phương trình tiếp tuyến của đường hypebol \(y=\frac{1}{x}\) tại điểm \(\left ( \frac{1}{2};2 \right )\) là:
\(y-2=-4(x-\frac{1}{2})\) hay \(y=-4x+4\)
Câu b:
Tại \(x_0=-1\Rightarrow y_0=y(-1)=-1\) và \(y'(-1)=-1\)
Vậy phương trình tiếp tuyến của đường hypebol \(y=\frac{1}{x}\) tại điểm có hoành độ -1 là:
\(y-y_0=y'(x_0)(x-x_0)\)
Hay \(y+1=-1(x+1)\Leftrightarrow y=-x-2.\)
Câu c:
Do hệ số góc của tiếp tuyến bằng \(-\frac{1}{4}\), nên
\(-\frac{1}{x^2_0}=-\frac{1}{4}\Leftrightarrow x_0=\pm 2.\)
Với \(x_0=2\Rightarrow y_0=\frac{1}{2}.\)
Vậy phương trình tiếp tuyến là:
\(y-y_0=-\frac{1}{4}(x-x_0)\) hay \(y-\frac{1}{2}=-\frac{1}{4}(x-2)\)
\(\Leftrightarrow y=-\frac{1}{4}x+1\)
Với \(x_0=-2\Rightarrow y_0=-\frac{1}{2}.\)
Vậy phương trình tiếp tuyến là:
\(y-y_0=-\frac{1}{4}(x-x_0)\) hay \(y+\frac{1}{2}=-\frac{1}{4}(x+2)\)
\(\Leftrightarrow y=-\frac{1}{4}x-1\).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 4 trang 156 SGK Đại số & Giải tích 11
Bài tập 5 trang 156 SGK Đại số & Giải tích 11
Bài tập 7 trang 157 SGK Đại số & Giải tích 11
Bài tập 5.1 trang 198 SBT Toán 11
Bài tập 5.2 trang 198 SBT Toán 11
Bài tập 5.3 trang 198 SBT Toán 11
Bài tập 5.4 trang 198 SBT Toán 11
Bài tập 5.5 trang 198 SBT Toán 11
Bài tập 5.6 trang 198 SBT Toán 11
Bài tập 5.7 trang 199 SBT Toán 11
Bài tập 5.8 trang 199 SBT Toán 11
Bài tập 5.9 trang 199 SBT Toán 11
Bài tập 5.10 trang 199 SBT Toán 11
Bài tập 5.11 trang 199 SBT Toán 11
Bài tập 1 trang 192 SGK Toán 11 NC
Bài tập 2 trang 192 SGK Toán 11 NC
Bài tập 3 trang 192 SGK Toán 11 NC
Bài tập 4 trang 192 SGK Toán 11 NC
Bài tập 5 trang 192 SGK Toán 11 NC
Bài tập 6 trang 192 SGK Toán 11 NC
Bài tập 7 trang 192 SGK Toán 11 NC
Bài tập 8 trang 192 SGK Toán 11 NC
Bài tập 9 trang 192 SGK Toán 11 NC
Bài tập 10 trang 195 SGK Toán 11 NC
Bài tập 11 trang 195 SGK Toán 11 NC
Bài tập 12 trang 195 SGK Toán 11 NC
Bài tập 13 trang 195 SGK Toán 11 NC
-


Viết phương trình tiếp tuyến của đồ thị hàm số y=3x+1/x+2, biết tiếp tuyến cách điểm I(-2;3) một khoảng lớn nhất
bởi Cua Yến
 04/04/2021
04/04/2021
Viết phương trình tiếp tuyến của đồ thị hàm số
y=3x+1/x+2 biết tiếp tuyến cách điểm I(-2;3) một khoảng lớn nhất
Theo dõi (0) 4 Trả lời -


Cho hàm số y=x^2 x.Tìm đạo hàm của hàm số trên khoảng ( âm vô cùng,dương vô cùng).
bởi May Phạm
 30/03/2021
30/03/2021
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho y=f(x)=2x.Tính f'(-1)
bởi An Bình
 10/03/2021
10/03/2021
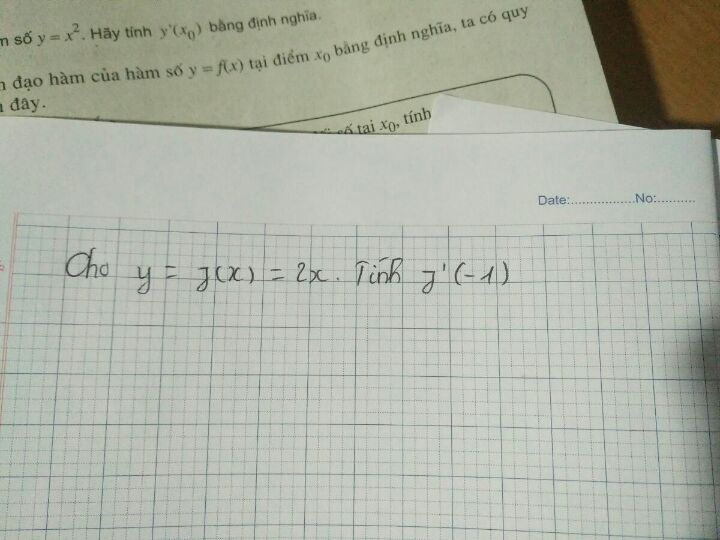 Theo dõi (2) 3 Trả lời
Theo dõi (2) 3 Trả lời -


Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \sqrt {2x + 1} \), biết hệ số góc của tiếp tuyến bằng 1/3.
bởi Nguyễn Thanh Trà
 01/03/2021
01/03/2021
A. \(y = \dfrac{x}{2} + \dfrac{5}{3}\)
B. \(y = \dfrac{x}{3} - \dfrac{5}{3}\)
C. \(y = \dfrac{x}{3} + \dfrac{5}{3}\)
D. \(y = x - 1\)
Theo dõi (0) 1 Trả lời





