Phần hướng dẫn giải bài tập SGK Toán 9 Bài 5 Công thức nghiệm thu gọn sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 9.
-
Bài tập 17 trang 49 SGK Toán 9 Tập 2
Xác định a, b', c rồi dùng công thức nghiệm thu gọn giải các phương trình:
a) \(4x^2 + 4x + 1 = 0\)
b) \(13852x^2 - 14x + 1 = 0\)
c) \(5x^2 - 6x + 1 = 0\)
d) \(-3x^2 + 4\sqrt{6}x + 4 = 0\)
-
Bài tập 18 trang 49 SGK Toán 9 Tập 2
Đưa các phương trình sau về dạng \(ax^2 + 2b'x + c = 0\) và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):
a) \(3x^2 -2x = x^2 + 3\)
b) \((2x - \sqrt{2})^2 - 1 = (x + 1)(x - 1)\)
c) \(3x^2 + 3 = 2(x + 1)\)
d) \(0,5x(x + 1) = (x - 1)^2\)
-
Bài tập 19 trang 49 SGK Toán 9 Tập 2
Đố em biết vì sao khi a > 0 và phương trình ax2 + bx + c = 0 vô nghiệm thì ax2 + bx + c > 0 với mọi giá trị của x?
-
Bài tập 20 trang 49 SGK Toán 9 Tập 2
Giải các phương trình:
a) \(25x^2 - 16 = 0\)
b) \(2x^2 + 3 = 0\)
c) \(4,2x^2 + 5,46x = 0\)
d) \(4x^2 - 2\sqrt{3}x = 1 -\sqrt{ 3}\)
- VIDEOYOMEDIA
-
Bài tập 21 trang 49 SGK Toán 9 Tập 2
Giải vài phương trình của An Khô-va-ri-zmi (Xem Toán 7, Tập 2, tr.26):
a) \(x^2 = 12x + 288\)
b) \(\frac{1}{12}x^2+\frac{7}{12}x=19\)
-
Bài tập 22 trang 49 SGK Toán 9 Tập 2
Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm:
a) \(15x^2 + 4x - 2005 = 0\)
b) \(-\frac{19}{5}x^2 - \sqrt{7}x + 1890 = 0\)
-
Bài tập 23 trang 50 SGK Toán 9 Tập 2
Rađa của một máy bay trực thăng theo dõi chuyển động của một ôtô trong 10 phút, phát hiện rằng vận tốc v của ôtô thay đổi phụ thuộc vào thời gian bởi công thức: \(\small v = 3t^2 - 30t + 135\)
(t tính bằng phút, v tính bằng km/h).
a) Tính vận tốc của ôtô khi t = 5 phút.
b) Tính giá trị của t khi vận tốc ôtô bằng 120 km/h (làm tròn kết quả đến chữ số thập phân thứ hai)
-
Bài tập 24 trang 50 SGK Toán 9 Tập 2
Cho phương trình (ẩn x) \(x^2 - 2(m - 1)x + m^2 = 0.\)
a) Tính \(\Delta '\)
b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệt ? Có nghiệm kép? Vô nghiệm?
-
Bài tập 27 trang 55 SBT Toán 9 Tập 2
Xác định a, b’, c trong mỗi phương trình, rồi giải phương trình bằng công thức nghiệm thu gọn:
a) \(5{x^2} - 6x - 1 = 0\)
b) \( - 3{x^2} + 14x - 8 = 0\)
c) \(- 7{x^2} + 4x = 3\)
d) \(9{x^2} + 6x + 1 = 0\)
-
Bài tập 28 trang 55 SBT Toán 9 Tập 2
Với những giá trị nào của x thì giá trị của hai biểu thức bằng nhau:
a) \({x^2} + 2 + 2\sqrt 2 \) và \(2\left( {1 + \sqrt 2 } \right)x\)
b) \(\sqrt 3 {x^2} + 2x - 1\) và \(2\sqrt 3 x + 3\)
c) \( - 2\sqrt 2 x - 1\) và \(\sqrt 2 {x^2} + 2x + 3\)
d) \({x^2} - 2\sqrt 3 x - \sqrt 3 \) và \(2{x^2} + 2x + \sqrt 3 \)
e) \(\sqrt 3 {x^2} + 2\sqrt 5 x - 3\sqrt 3 \) và \( - {x^2} - 2\sqrt 3 x + 2\sqrt 5 + 1\)?
-
Bài tập 29 trang 55 SBT Toán 9 Tập 2
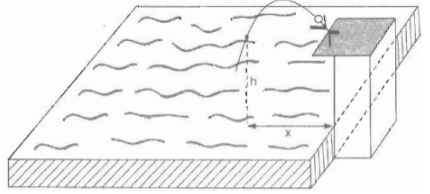
Một vận động viên bơi lội nhảy cầu (xem hình 5). Khi nhảy, độ cao h từ người đó tới mặt nước (tính bằng mét) phụ thuộc vào khoảng cách x từ điểm rơi đến chân cầu (tính bằng mét) bởi công thức:
\(h = - {\left( {x - 1} \right)^2} + 4\)
Hỏi khoảng cách x bằng bao nhiêu
a) Khi vận động viên ở độ cao 3m?
b) Khi vận động viên chạm mặt nước?
-
Bài tập 30 trang 56 SBT Toán 9 Tập 2
Tính gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai):
a) \(16{x^2} - 8x + 1 = 0\)
b) \(6{x^2} - 10x - 1 = 0\)
c) \(5{x^2} + 24x + 9 = 0\)
d) \(16{x^2} - 10x + 1 = 0\)
-
Bài tập 31 trang 56 SBT Toán 9 Tập 2
Với giá trị nào của x thì giá trị của hai hàm số bằng nhau:
a) \(y = {1 \over 3}{x^2}\) và \(y = 2x - 3\)
b) \(y = - {1 \over 2}{x^2}\) và \(y = x - 8\)?
-
Bài tập 32 trang 56 SBT Toán 9 Tập 2
Với giá trị nào của m thì:
a) Phương trình \(2{x^2} - {m^2}x + 18m = 0\) có một nghiệm x = -3.
b) Phương trình \(m{x^2} - x - 5{m^2} = 0\) có một nghiệm x = -2?
-
Bài tập 33 trang 56 SBT Toán 9 Tập 2
Với giá trị nào của m thì phương trình có hai nghiệm phân biệt:
a) \({x^2} - 2\left( {m + 3} \right)x + {m^2} + 3 = 0\)
b) \(\left( {m + 1} \right){x^2} + 4mx + 4m - 1 = 0\)
-
Bài tập 34 trang 56 SBT Toán 9 Tập 2
Với giá trị nào của m thì phương trình có nghiệm kép:
a) \(5{x^2} + 2mx - 2m + 15 = 0\)
b) \(m{x^2} - 4\left( {m - 1} \right)x - 8 = 0\)
-
Bài tập 5.1 trang 56 SBT Toán 9 Tập 2
Giả sử \({x_1} , {x_2}\) là hai nghiệm của phương trình bậc hai \(a{x^2} + bx + c = 0\) có \(∆’ = 0\). Điều nào sau đây là đúng?
A) \(\displaystyle {x_1} = {x_2} = {b \over {2a}}\)
B) \(\displaystyle {x_1} = {x_2} = - {{b'} \over a}\)
C) \(\displaystyle {x_1} = {x_2} = - {b \over a}\)
D) \(\displaystyle {x_1} = {x_2} = - {{b'} \over {2a}}\)
-
Bài tập 5.2 trang 56 SBT Toán 9 Tập 2
Tìm mối liên hệ giữa \(a, b, c\) để phương trình \(\left( {{b^2} + {c^2}} \right){x^2} - 2acx + {a^2} - {b^2} = 0\) có nghiệm.
-
Bài tập 5.3 trang 56 SBT Toán 9 Tập 2
Chứng tỏ rằng phương trình \(\left( {x - a} \right)\left( {x - b} \right) + \left( {x - b} \right)\left( {x - c} \right) \) \(+ \left( {x - c} \right)\left( {x - a} \right) = 0\) luôn có nghiệm.





